练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数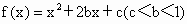，f(1)=0，且方程f(x)＋1=0有实根．

    (1)证明－3＜c≤－1，b≥0．

    (2)若m是方程f(x)＋1=0的一个实根，判断f(m－4)的正负并加以证明．

    答案：略
    解析：

    证明：(1)，

    又1＞b＞c，故，

    方程f(x)＋1=0有实根，

    即有实根，

    故，

    即，

    ∴．

    由知．

    (2)

    ∵f(x)=－1＜0，

    ∴c＜m＜1，如图所示．

    ∴c－4＜m－4＜－3－c．

    ∴f(m－4)=(m－4－c)(m－4－1)＞0．

    ∴f(m－4)的符号为正．


    提示：

    在解题过程中常利用图形增加直观性．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    设函数满足f (-1)=2，则它在　　　

    [　　]

    A．区间[0，+∞)是增函数　　　     B．区间(-∞，0]是减函数

    C．区间(-∞，+∞)是奇函数　　　 D．区间(-∞，+∞)是偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    设函数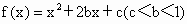，f(1)=0，且方程f(x)＋1=0有实根．

    (1)证明－3＜c≤－1，b≥0．

    (2)若m是方程f(x)＋1=0的一个实根，判断f(m－4)的正负并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)在(－∞,0)∪(0,+∞)上有定义，且在(0,+∞)上是增函数，f(1)=0,又g(θ)=sin2θ－mcosθ－2m,θ∈［0,］,设M={m|g(θ)<0,m∈R},N={m|f［g(θ)］<0},求M∩N.

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年山东省高三上学期第一次诊断性测试理科数学卷 题型：选择题

    设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式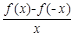＜0的解集是

    A.(-1,0)∪(1,+∞)                       B.(-∞,-1) ∪(0,1)

    C.(-∞,-1)∪(1,+∞)                     D.(-1,0)∪(0,1)

     

    查看答案和解析>>

    同步练习册答案