
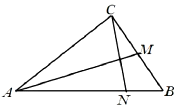
 如图,在△ABC中,M为BC的中点,$\overrightarrow{AN}=3\overrightarrow{NB}$.
如图,在△ABC中,M为BC的中点,$\overrightarrow{AN}=3\overrightarrow{NB}$.分析 (Ⅰ)根据向量的几何意义即可求出,
(Ⅱ)根据向量的垂直和向量的数量积公式即可求出答案.
解答 解:(Ⅰ)$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}$;
$\overrightarrow{CN}=\overrightarrow{CA}+\overrightarrow{AN}=\overrightarrow{CA}+\frac{3}{4}\overrightarrow{AB}=\overrightarrow{CA}+\frac{3}{4}(\overrightarrow{CB}-\overrightarrow{CA})=\frac{1}{4}\overrightarrow{CA}+\frac{3}{4}\overrightarrow{CB}$,
(Ⅱ)由已知AM⊥CN,得$\overline{AM}•\overrightarrow{CN}=0$,即$(-\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB})•(\frac{1}{4}\overrightarrow{CA}+\frac{3}{8}\overrightarrow{CB})=0$,
展开得 $-\frac{1}{4}{\overrightarrow{CA}^2}-\frac{5}{8}\overrightarrow{CA}•\overrightarrow{CB}+\frac{3}{8}{\overrightarrow{CB}^2}=0$,
又∵∠ACB=120°,CB=4,
∴${|{\overrightarrow{CA}}|^2}-5|{\overrightarrow{CA}}|-24=0$,
即$(|{\overrightarrow{CA}}|-8)(|{\overrightarrow{CA}}|+3)=0$,
解得$|{\overrightarrow{CA}}|=8$,即CA=8为所求
点评 本题考查了向量的几何意义和向量的垂直和向量的数量积的运算,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | a+c>b+c | C. | ac>bc | D. | $\frac{1}{a}$>$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com