
(本小题12分) 已知二次函数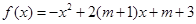 与
与 轴有两个交点
轴有两个交点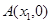 和
和 ,若,且
,若,且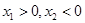
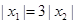 .
.
(Ⅰ)求此二次函数的解析式
(Ⅱ)若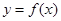 在闭区间
在闭区间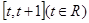 的最大值为
的最大值为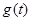 ,求
,求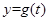 的解析式及其最大值
的解析式及其最大值
科目:高中数学 来源: 题型:解答题
(本小题满分13分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度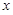 (单位:cm)满足关系:
(单位:cm)满足关系: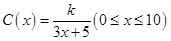 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设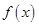 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求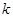 的值及
的值及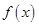 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用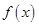 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
某漁业公司年初用98万元购买一艘捕魚船,第一年各种支出费用12万元,以后每年都增加
4万元,每年捕魚收益50万元.
(1)该公司第几年开始获利?
(2)若干年后,有两种处理方案:
①年平均获利最大时,以26万元出售该渔船;
②总纯收入获利最大时,以8万元出售渔船.
问哪种处理方案最合算?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
15分)经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间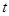 (天)的函数,且销售量近似满足函数
(天)的函数,且销售量近似满足函数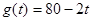 (件),价格近似满足函数
(件),价格近似满足函数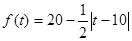 (元)。
(元)。
(1)试写出该种商品的日销售额 函数表达式;
函数表达式;
(2)求该种商品的日销售额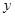 的最大值与最小值。
的最大值与最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施,将 个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
| 时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 病毒细胞总数(个) |  | 2 | 4 | 8 | 16 | 32 | 64 |

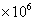 个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.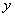 与时间
与时间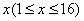 的函数关系式;
的函数关系式; )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com