
分析 (1)由抛物线的定义可得点Q的轨迹是以F为焦点,以直线l1:x=-1为准线的抛物线,即可求曲线T的方程;
(2)设AB的方程为y=k1(x-2),联立抛物线方程得k1y2-4y-8k1=0,y1+y2=$\frac{4}{{k}_{1}}$,y1y2=-4m,求出M,N的坐标,由此能证明直线MN恒过定点(2,2).
解答 (1)解:过点P作l的垂线与线段PF的垂直平分线相交于点Q,∴|QP|=|QF|,即点Q到点F(1,0)的距离等于点Q到直线l1:x=-1的距离,
由抛物线的定义可得点Q的轨迹是以F为焦点,以直线l1:x=-1为准线的抛物线,
方程为y2=4x.
(2)证明:设AB的方程为y=k1(x-2),联立抛物线方程得k1y2-4y-8k1=0,y1+y2=$\frac{4}{{k}_{1}}$,y1y2=-4m,
AB中点M($\frac{2}{{{k}_{1}}^{2}}$+2,$\frac{2}{{k}_{1}}$),
同理,点N($\frac{2}{{{k}_{2}}^{2}}$+2,$\frac{2}{{k}_{2}}$),
∴kMN=$\frac{{k}_{1}{k}_{2}}{{k}_{1}+{k}_{2}}$=k1k2,
∴MN:y-$\frac{2}{{k}_{1}}$=k1k2[x-($\frac{2}{{{k}_{1}}^{2}}$+2)],
即y=k1k2(x-2)+2,
∴直线MN恒过定点(2,2).
点评 本题考查点的轨迹方程的求法,考查直线过定点的证明,解题时要认真审题,注意中点坐标公式的合理运用.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直.
如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
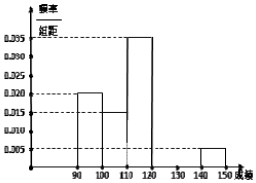 某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com