
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点. 
(1)求证:EF∥面PBC
(2)求证:平面PBC⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos2α+cos2β=1类比到空间,在长方体中,一条对角线与从其一顶点出发的三个面所成的角分别为α,β,γ,则有cos2α+cos2β+cos2γ= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
近视度数 | 0﹣100 | 100﹣200 | 200﹣300 | 300﹣400 | 400以上 |
学生频数 | 30 | 40 | 20 | 10 | 0 |
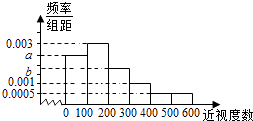
将近视程度由低到高分为4个等级:当近视度数在0﹣100时,称为不近视,记作0;当近视度数在100﹣200时,称为轻度近视,记作1;当近视度数在200﹣400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(1)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(2)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(3)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在(0,+
在(0,+![]() )上恒成立,求实数
)上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值;
(3)在棱AD上是否存在一点P,使得BP∥平面AD1E?若存在,求DP的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax,g(x)=lnx,h(x)=f(x)+g(x)
(1)若f(x)≥g(x)对于公共定义域内的任意x恒成立,求实数a的取值范围;
(2)设h(x)有两个极值点x1 , x2 , 且x1∈(0, ![]() ),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com