
【题目】如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD, ![]() ,M为PC的中点,N点在AB上且
,M为PC的中点,N点在AB上且![]() .
.
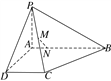
(1)证明:MN∥平面PAD;
(2)求直线MN与平面PCB所成的角.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)过点M作ME∥CD交PD于E点,则根据平几知识可得AEMN为平行四边形,即EM∥AN,再根据线面平行判定定理证结论(2)过N点作NQ∥AP交BP于点Q, NF⊥CB于点F,则易得面NQF垂直平面PCB,再过N点作NH⊥QF于点H,由面面垂直性质定理得NH⊥平面PBC,因此可得∠NMH为直线MN与平面PCB所成角,最后解三角形得直线MN与平面PCB所成的角.
试题解析:证明 (1)过点M作ME∥CD交PD于E点,连接AE,
∵AN=![]() NB,∴AN=
NB,∴AN=![]() AB=
AB=![]() DC=EM,
DC=EM,
又EM∥DC∥AB,∴EM∥AN,
∴四边形AEMN为平行四边形,∴MN∥AE,
又∵AE平面PAD,MN平面PAD,∴MN∥平面PAD.
(2)过N点作NQ∥AP交BP于点Q,
NF⊥CB于点F,连接QF,过N点作NH⊥QF于点H,
连接MH,易知QN⊥平面ABCD,
∴QN⊥BC,又NF⊥BC,NF∩QN=N,NF平面QNF,QN平面QNF,
∴BC⊥平面QNF,∴BC⊥NH,
∵NH⊥QF,BC∩QF=F,BC平面PBC,QF平面PBC,∴NH⊥平面PBC,
∴∠NMH为直线MN与平面PCB所成角,
通过计算可得MN=AE=![]() ,QN=
,QN=![]() ,NF=
,NF=![]()
![]() ,
,
∴NH=![]() =
=![]() =
=![]() ,
,
∴sin∠NMH=![]() =
=![]() ,∴∠NMH=60°,∴直线MN与平面PCB所成角为60°.
,∴∠NMH=60°,∴直线MN与平面PCB所成角为60°.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若对定义域内的任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的值;
的值;
(2)若函数![]() 的定义域上是单调函数,求实数
的定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意的正整数
,证明对任意的正整数![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·鸡西一模)在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足![]() 的实数λ的值有( )
的实数λ的值有( )
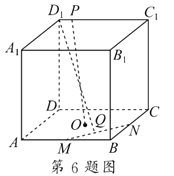
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() x3-kx,其中实数k为常数.
x3-kx,其中实数k为常数.
(1)当k=4时,求函数的单调区间;
(2)若曲线y=f(x)与直线y=k只有一个交点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若销售金额(单位:万元)不低于平均值![]() 的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
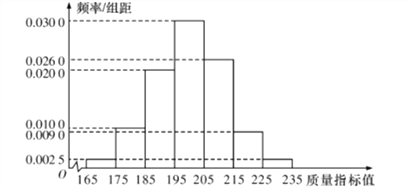
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com