
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,半焦距为
,半焦距为![]() ,过点
,过点![]() 作
作![]() 轴、
轴、![]() 轴的垂线,垂足分别点
轴的垂线,垂足分别点![]() ,
,![]() ,且四边形
,且四边形![]() 的面积为2.
的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,设直线
两点,设直线![]() 与直线
与直线![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
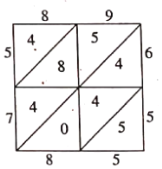
【题目】写算,是一种格子乘法,也是笔算乘法的一种,用以区别筹算与珠算,它由明代数学家吴敬在其撰写的《九章算法比类大全》一书中提出,是从天元式的乘法演变而来.例如计算![]() ,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出
,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出![]() 的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查防疫期间学生居家每天锻炼时间情况,从高一、高二年级学生中分别随机抽取100人,由调查结果得到如下的频率分布直方图:
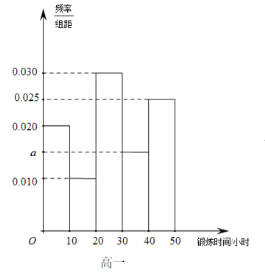
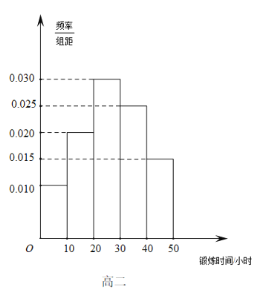
(Ⅰ)写出频率分布直方图(高一)中![]() 的值;记高一、高二学生100人锻炼时间的样本的方差分别为
的值;记高一、高二学生100人锻炼时间的样本的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出结论);
的大小(只要求写出结论);
(Ⅱ)估计在高一、高二学生中各随机抽取1人,恰有一人的锻炼时间大于20分钟的概率;
(Ⅲ)由频率分布直方图可以认为,高二学生锻炼时间![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差,且每名学生锻炼时间相互独立,设
近似为样本方差,且每名学生锻炼时间相互独立,设![]() 表示从高二学生中随机抽取10人,其锻炼时间位于
表示从高二学生中随机抽取10人,其锻炼时间位于![]() 的人数,求
的人数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]()
②若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
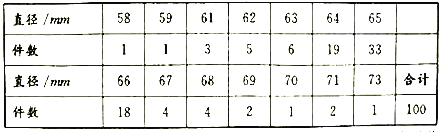
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):
表示相应事件的概率):
①![]() ;
;
②![]() ;
;
③![]() .
.
判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为了.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”.
之外的零件认定为是“次品”.
①从设备![]() 的生产流水线上随机抽取2个零件,求其中次品个数
的生产流水线上随机抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月20日,第六届世界互联网大会发布了15项“世界互联网领先科技成果”,其中有5项成果均属于芯片领域,分别为华为高性能服务器芯片“鲲鹏920”、清华大学“面向通用人工智能的异构融合天机芯片”、“特斯拉全自动驾驶芯片”、寒武纪云端AI芯片、“思元270”、赛灵思“Versal自适应计算加速平台”.现有3名学生从这15项“世界互联网领先科技成果”中分别任选1项进行了解,且学生之间的选择互不影响,则至少有1名学生选择“芯片领域”的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为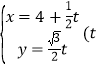 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com