设函数f(x)=x2+aln(1+x)有两个极值点x1、x2,且x1<x2.
(I)求a的取值范围,并讨论f(x)的单调性;
(II)求f(x2)的取值范围.
解:(I)求导函数可得f′(x)=
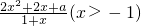
令g(x)=2x
2+2x+a,,其对称轴为x=-

.
由题意知x
1、x
2是方程g(x)=0的两个均大于-1的不相等的实根,
其充要条件为△=4-8a>0且g(-1)=a>0,得0<a<

…(2分)
(1)当x∈(-1,x
1)时,f'(x)>0,∴f(x)在(-1,x
1)内为增函数;
(2)当x∈(x
1,x
2)时,f'(x)<0,∴f(x)在(x
1,x
2)内为减函数;
(3)当x∈(x
2,+∞)时,f'(x)>0,∴f(x)在(x
2,+∞)内为增函数;
(II)由(I)g(0)=a>0,∴-

<x
2<0,a=-(2x
22+2x
2)
∴f(x
2)=x
22+aln(1+x
2)=x
22-(2x
22+2x
2)ln(1+x
2)
设h(x)=x
2-(2x
2+2x)ln(1+x)(x>-

),…(8分)
则h'(x)=2x-2(2x+1)ln(1+x)-2x=-2(2x+1)ln(1+x)…(10分)
(1)当x∈(-

,0)时,h'(x)>0,∴h(x)在(-

,0)单调递增;
(2)当x∈(0,+∞)时,h'(x)<0,h(x)在(0,+∞)单调递减 …(12分)
∴当x∈(-

,0)时,h(x)>h(-

)=
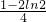
故f(x
2)=h(x
2)>
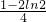
. …(14分)
分析:(I)先确定函数的定义域然后求导数f′(x),令g(x)=2x
2+2x+a,由题意知x
1、x
2是方程g(x)=0的两个均大于-1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式f′(x)>0和f′(x)<0,求出单调区间;
(II)x
2是方程g(x)=0的根,将a用x
2表示,消去a得到关于x
2的函数,研究函数的单调性求出函数的最大值,即可求f(x
2)的取值范围.
点评:本题主要考查了利用导数研究函数的单调性,以及利用导数研究函数的极值等有关知识,属于中档题.

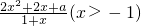
 .
. …(2分)
…(2分) <x2<0,a=-(2x22+2x2)
<x2<0,a=-(2x22+2x2) ),…(8分)
),…(8分) ,0)时,h'(x)>0,∴h(x)在(-
,0)时,h'(x)>0,∴h(x)在(- ,0)单调递增;
,0)单调递增; ,0)时,h(x)>h(-
,0)时,h(x)>h(- )=
)=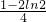
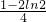 . …(14分)
. …(14分)

 名校课堂系列答案
名校课堂系列答案