
【题目】如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.

(Ⅰ)求证:BC⊥A1D;
(Ⅱ)求证:平面A1BC⊥平面A1BD;
(Ⅲ)求点C到平面A1BD的距离.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】
试题(Ⅰ)由线面垂直得A1O⊥BC,再由BC⊥DC,能证明BC⊥A1D.
(Ⅱ)由BC⊥A1D,A1D⊥A1B,得A1D⊥平面A1BC,由此能证明平面A1BC⊥平面A1BD.
(Ⅲ)由![]() =
=![]() ,能求出点C到平面A1BD的距离.
,能求出点C到平面A1BD的距离.
证明:(Ⅰ)∵A1O⊥平面DBC,∴A1O⊥BC,
又∵BC⊥DC,A1O∩DC=O,
∴BC⊥平面A1DC,∴BC⊥A1D.
(Ⅱ)∵BC⊥A1D,A1D⊥A1B,BC∩A1B=B,
∴A1D⊥平面A1BC,
又∵A1D平面A1BD,
∴平面A1BC⊥平面A1BD.
解:(Ⅲ)设C到平面A1BD的距离为h,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵![]() =S△DBC,
=S△DBC,![]() ,∴
,∴![]() .
.
∴点C到平面A1BD的距离为![]() .
.



 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
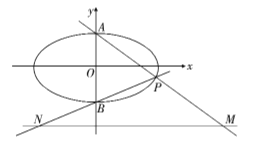
【题目】如图,已知椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上,且异于点
在椭圆上,且异于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与直线
与直线![]() :
: ![]() 分别交于点
分别交于点![]() 、
、![]() ,且
,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 的长的最小值.
的长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点.
的中点.

(1)求证:![]()
![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)判断直线![]() 与平面
与平面![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com