
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
【答案】19. 解①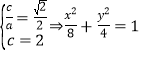
②设![]()
![]()
由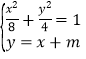
![]()
![]()
![]()
又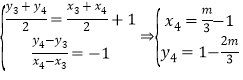 在
在![]() 上
上
![]()
![]()
![]() 或
或![]()
经检验解题
![]() 或
或![]()
【解析】
本试题主要是考查了椭圆方程的求解,以及直线与椭圆的位置关系的运用。
(1)由题意,得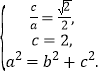 得到a,b,c的值。得到椭圆的方程。
得到a,b,c的值。得到椭圆的方程。
(2)设点A、B的坐标分别为(x1,y1),(x2, y2),线段AB的中点为M(x0,y0),
由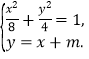 消y得,3x2+4mx+2m2-8=0结合韦达定理,和判别式得到参数m值。
消y得,3x2+4mx+2m2-8=0结合韦达定理,和判别式得到参数m值。
解:(1) 由题意,得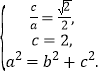 ………………………………………………3分
………………………………………………3分
解得![]() ∴椭圆C的方程为
∴椭圆C的方程为![]() .…………………………………………6分
.…………………………………………6分
(2) 设点A、B的坐标分别为(x1,y1),(x2, y2),线段AB的中点为M(x0,y0),
由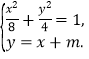 消y得,3x2+4mx+2m2-8=0,……………………………………………8分
消y得,3x2+4mx+2m2-8=0,……………………………………………8分
Δ=96-8m2>0,∴-2![]() <m<2
<m<2![]() .
.
∴![]()
![]() .………………………………………12分
.………………………………………12分
∵点M(x0,y0)在圆x2+y2=1上,
![]() ,
,![]() .………………………………………………… 14分
.………………………………………………… 14分


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+
=1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+ ![]() =1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
=1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足 ![]() ,(O为坐标原点),求实数λ取值范围.
,(O为坐标原点),求实数λ取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 E: ![]() .
.
(I)求曲线 E的离心率及标准方程;
(II)设 M(x0 , y0)是曲线 E上的任意一点,过原点作⊙M:(x﹣x0)2+(y﹣y0)2=8的两条切线,分别交曲线 E于点 P、Q.
①若直线OP,OQ的斜率存在分别为k1 , k2 , 求证:k1k2=﹣ ![]() ;
;
②试问OP2+OQ2是否为定值.若是求出这个定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图ABCD是平面四边形,∠ADB=∠BCD=90°,AB=4,BD=2.
(Ⅰ)若BC=1,求AC的长;
(Ⅱ)若∠ACD=30°,求tan∠BDC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体P﹣ABC中,PA=4,AC=2 ![]() ,PB=BC=2
,PB=BC=2 ![]() ,PA⊥平面PBC,则四面体P﹣ABC的外接球半径为( )
,PA⊥平面PBC,则四面体P﹣ABC的外接球半径为( )
A.2 ![]()
B.2 ![]()
C.4 ![]()
D.4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且对任意正整数n都有an是n与Sn的等差中项,bn=an+1.
(1)求证:数列{bn}是等比数列,并求出其通项bn;
(2)若数列{Cn}满足Cn= ![]() 且数列{C
且数列{C ![]() }的前n项和为Tn , 证明Tn<2.
}的前n项和为Tn , 证明Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体P﹣ABC中,PA=4,AC=2 ![]() ,PB=BC=2
,PB=BC=2 ![]() ,PA⊥平面PBC,则四面体P﹣ABC的外接球半径为( )
,PA⊥平面PBC,则四面体P﹣ABC的外接球半径为( )
A.2 ![]()
B.2 ![]()
C.4 ![]()
D.4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a2=3,a5=81,bn=1+2log3an .
(1)求数列{bn}的前n项的和;
(2)已知数列 ![]() 的前项的和为Sn , 证明:
的前项的和为Sn , 证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com