
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上成立,求
上成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】为响应市政府提出的以新旧动能转换为主题的发展战略,某公司花费100万元成本购买了1套新设备用于扩大生产,预计该设备每年收入100万元,第一年该设备的各种消耗成本为8万元,且从第二年开始每年比上一年消耗成本增加8万元.
(1)求该设备使用x年的总利润y(万元)与使用年数x(x∈N*)的函数关系式(总利润=总收入﹣总成本);
(2)这套设备使用多少年,可使年平均利润最大?并求出年平均利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),过点
为参数),过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的值;
的值;
(2)求线段![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第![]() 周)和市场占有率(
周)和市场占有率(![]() )的几组相关数据如下表:
)的几组相关数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据上述线性回归方程,预测在第几周,该款旗舰机型市场占有率将首次超过![]() (最后结果精确到整数).
(最后结果精确到整数).
参考公式: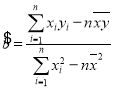 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,连接
,连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 时,求二面角
时,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数学建模课上,老师给大家带来了一则新闻:“2019年8月16日上午,423米的东莞第一高楼民盈国贸中心2号楼(以下简称“国贸中心”)正式封顶,随着最后一方混凝土浇筑到位,标志着东莞最高楼纪录诞生,由东莞本地航母级企业民盈集团刷新了东莞天际线,比之前的东莞第一高楼台商大厦高出134米.”在同学们的惊叹中,老师提出了问题:国贸中心真有这么高吗?我们能否运用所学知识测量验证一下?一周后,两个兴趣小组分享了他们各自的测量方案.
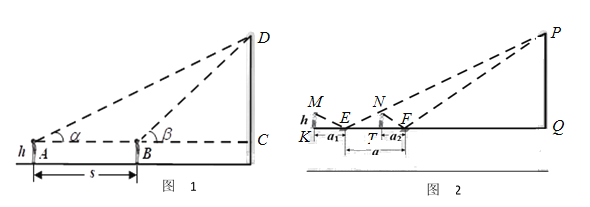
第一小组采用的是“两次测角法”:他们在国贸中心隔壁的会展中心广场上的![]() 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为![]() ,正对国贸中心前进了
,正对国贸中心前进了![]() 米后,到达
米后,到达![]() 点,在
点,在![]() 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为![]() ,然后计算出国贸中心的高度(如图).
,然后计算出国贸中心的高度(如图).
第二小组采用的是“镜面反射法”:在国贸中心后面的新世纪豪园一幢11层楼(与国贸中心处于同一水平面,每层约3米)楼顶天台上,进行两个操作步骤:①将平面镜置于天台地面上,人后退至从镜中能看到国贸大厦的顶部位置,测量出人与镜子的距离为![]() 米;②正对国贸中心,将镜子前移
米;②正对国贸中心,将镜子前移![]() 米,重复①中的操作,测量出人与镜子的距离为
米,重复①中的操作,测量出人与镜子的距离为![]() 米.然后计算出国贸中心的高度(如图).
米.然后计算出国贸中心的高度(如图).
实际操作中,第一小组测得![]() 米,
米,![]() ,
,![]() ,最终算得国贸中心高度为
,最终算得国贸中心高度为![]() ;第二小组测得
;第二小组测得![]() 米,
米,![]() 米,
米,![]() 米,最终算得国贸中心高度为
米,最终算得国贸中心高度为![]() ;假设他们测量者的“眼高
;假设他们测量者的“眼高![]() ”都为
”都为![]() 米.
米.
(1)请你用所学知识帮两个小组完成计算(参考数据:![]() ,
,![]() ,答案保留整数结果);
,答案保留整数结果);
(2)你认为哪个小组的方案更好,说出你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.![]() 是空间中的四点,若
是空间中的四点,若![]() 不能构成空间基底,则
不能构成空间基底,则![]() 共面
共面
B.已知![]() 为空间的一个基底,若
为空间的一个基底,若![]() ,则
,则![]() 也是空间的基底
也是空间的基底
C.若直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,则直线
,则直线![]()
D.若直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,则直线
,则直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com