
分析 (1)求出以AB为直径的圆与x轴的交点,即可得到交点个数.
(2)利用平面几何中的圆外角小于圆周角,设过AB且与x轴相切的圆与x轴的切点为P,则P点即为所求的点.
解答 解:(1)点M在坐标轴上运动,满足MA⊥MB点,就是以AB为直径的圆与x轴的交点,
A(-1,2),B(1,4),圆心是AB的中点(0,3),半径为:$\sqrt{2}$.
以AB为直径的圆的方程为:x2+(y-3)2=2,y=0,解得方程无解,
若点M在坐标轴上运动,满足MA⊥MB点M的个数为0个.
故答案为:0.
(2)设过AB且与x轴相切的圆的圆心为E(x,y),则M(x,0).因为M,A,B三点在圆上,
∴EM=EA=EB,
∴(x+1)2+(y-2)2=y2=(x-1)2+(y-4)2
整理可得,x2+6x-7=0
解方程可得x=1,x=-7.M(1,0),(-7,0).
故答案为:M(1,0),(-7,0).
点评 本题主要考查了圆的性质圆外的角小于圆周角在求解角的最值中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
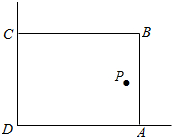 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com