
【题目】已知函数![]() (
(![]() ).
).
(1)求函数![]() 的单调区间;
的单调区间;
(2)试问:函数![]() 图像上是否存在不同两点
图像上是否存在不同两点![]() ,使得
,使得![]() 在
在![]() 处的切线
处的切线![]() 平行于直线
平行于直线![]() ,若存在,求出
,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析.
上单调递减;(2)证明见解析.
【解析】试题分析:
(1)结合函数的解析式可得![]() ,据此可得
,据此可得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)假设存在两点![]() ,不妨设
,不妨设![]() ,则
,则![]() ,且函数在
,且函数在![]() 处的切线斜率
处的切线斜率![]() ,据此整理计算有:
,据此整理计算有: 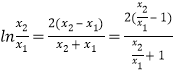 ,令
,令![]() ,则
,则![]() ,则:
,则:![]() ,
,![]() ,利用导函数研究函数的性质可得在
,利用导函数研究函数的性质可得在![]() 内不存在
内不存在![]() ,使得
,使得![]() ,则函数
,则函数![]() 图象上是不存在满足题意的点.
图象上是不存在满足题意的点.
试题解析:
(1)由![]() ,又
,又![]() 得
得![]()
故,当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,
,
![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)假设存在两点![]() ,不妨设
,不妨设![]() ,则:
,则:
![]() ,
,
![]() ,
,
故![]() =
=![]() ,
,
在函数图象![]() 处的切线斜率
处的切线斜率![]() ,
,
得:![]()
![]() ,
,
化简得:![]() ,
, 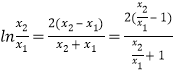 ,
,
令![]() ,则
,则![]() ,上式化为:
,上式化为:![]() ,即
,即![]() ,
,
若令![]() ,
,![]() ,
,
由![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
这表明在![]() 内不存在
内不存在![]() ,使得
,使得![]() .
.
综上,函数![]() 图象上是不存在不同两点
图象上是不存在不同两点![]() ,使得
,使得![]() 在
在![]() 处的切线
处的切线![]() 平行于直线
平行于直线![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱A1B1C1 - ABC中,侧棱AA1丄底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是

A. CC1与B1E是异面直线 B. AC丄平面ABB1A1
C. A1C1∥平面AB1E D. AE与B1C1为异面直线,且AE丄B1C1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若m﹣ ![]() <x
<x ![]() (m∈Z),则m叫做离实数x最近的整数,记作{x},即m={x},关于函数f(x)=x﹣{x}的四个命题:①定义域为R,值域为(﹣
(m∈Z),则m叫做离实数x最近的整数,记作{x},即m={x},关于函数f(x)=x﹣{x}的四个命题:①定义域为R,值域为(﹣ ![]() ,
, ![]() ]; ②点(k,0)是函数f(x)图象的对称中心(k∈Z);③函数f(x)的最小正周期为1; ④函数f(x)在(﹣
]; ②点(k,0)是函数f(x)图象的对称中心(k∈Z);③函数f(x)的最小正周期为1; ④函数f(x)在(﹣ ![]() ,
, ![]() ]上是增函数.上述命题中,真命题的序号是
]上是增函数.上述命题中,真命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为![]() ,
,![]() ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为![]() ,
,![]() ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈R,f(x)= ![]() 为奇函数.
为奇函数.
(1)求函数F(x)=f(x)+2x﹣ ![]() ﹣1的零点;
﹣1的零点;
(2)设g(x)=2log2( ![]() ),若不等式f﹣1(x)≤g(x)在区间[
),若不等式f﹣1(x)≤g(x)在区间[ ![]() ,
, ![]() ]上恒成立,求实数k的取值范围.
]上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①如果![]() ,
,![]() 是两条直线,且
是两条直线,且![]() ,那么
,那么![]() 平行于经过
平行于经过![]() 的任何平面;
的任何平面;
②如果直线![]() 和平面
和平面![]() 满足
满足![]() ,那么直线
,那么直线![]() 与平面
与平面![]() 内的任何直线平行;
内的任何直线平行;
③如果直线![]() ,
,![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,那么
,那么![]() ;
;
④如果直线![]() ,
,![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;
;
⑤如果平面![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,那么
,那么![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:![]() )的分组区间为
)的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将其按从左到右的顺序分别编号为第一组,第二组,
,将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.
,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  ,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
A.[3﹣2ln2,2)
B.[3﹣2ln2,2]
C.[e﹣1,2]
D.[e﹣1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com