
分析 不妨设$\overrightarrow{{F}_{1}}$=(a,0),(a>0)当他们的夹角为90°时,可得$\overrightarrow{{F}_{2}}$=(0,a).由于合力的大小为10N,可得$\sqrt{2}|\overrightarrow{{F}_{1}}|$=$\sqrt{2}$a=10,解得a.当他们的夹角是120°时,可得$\overrightarrow{{F}_{2}}$,即可得出$\overrightarrow{{F}_{1}}+\overrightarrow{{F}_{2}}$.
解答 解:不妨设$\overrightarrow{{F}_{1}}$=(a,0),(a>0)当他们的夹角为90°时,可得$\overrightarrow{{F}_{2}}$=(0,a),
∵合力的大小为10N,
∴$\sqrt{2}|\overrightarrow{{F}_{1}}|$=$\sqrt{2}$a=10,解得a=5$\sqrt{2}$.
当他们的夹角是120°时,$\overrightarrow{{F}_{2}}$=$(-\frac{5\sqrt{2}}{2},\frac{5\sqrt{6}}{2})$.
$\overrightarrow{{F}_{1}}+\overrightarrow{{F}_{2}}$=$(\frac{5\sqrt{2}}{2},\frac{5\sqrt{6}}{2})$.
则$|\overrightarrow{{F}_{1}}+\overrightarrow{{F}_{2}}|$=$\sqrt{(\frac{5\sqrt{2}}{2})^{2}+(\frac{5\sqrt{6}}{2})^{2}}$=$5\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 本题考查了向量平行四边形法则与向量的数量积运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
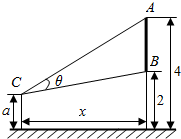 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{97}{16}$ | B. | $\frac{11}{2}$ | C. | $\frac{167}{28}$ | D. | $\frac{38}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z≥y>x | B. | z≥x>y | C. | x>z≥y | D. | z>x≥y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,5] | B. | [-8,2] | C. | [-4,1] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com