
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c.已知acosB﹣c= ![]() .
.
(1)求角A的大小;
(2)若b﹣c= ![]() ,a=3+
,a=3+ ![]() ,求BC边上的高.
,求BC边上的高.
【答案】
(1)解:由 ![]() 及正弦定理可得:
及正弦定理可得: ![]() ,
,
因为sinC=sin(A+B)=sinAcosB+cosAsinB,
所以 ![]() ,
,
因为sinB≠0,所以 ![]() ,
,
因为0<A<π,所以 ![]()
(2)解:由余弦定理可知: ![]() ,
,
所以: ![]() ,
,
解得: ![]() .
.
设BC边上的高为h,由 ![]() ,
,
得: ![]() ,
,
解得:h=1.
【解析】(1)由正弦定理及三角函数恒等变换化简已知等式可得cosAsinB= ![]() sinB,由sinB≠0,解得cosA,结合A的范围即可得解.(2)由余弦定理可解得:
sinB,由sinB≠0,解得cosA,结合A的范围即可得解.(2)由余弦定理可解得: ![]() ,设BC边上的高为h,由
,设BC边上的高为h,由 ![]() ,即可解得h的值.
,即可解得h的值.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)选修4-5:不等式选讲
已知函数f(x)=|x+1|-2|x-a|, a>0.
(1)当a=1时求不等式f(x)>1的解集;
(2)若f(x)图像与x轴围成的三角形面积大于6,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣ ![]() 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣ ![]() .
. 
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=![]() .
.
(Ⅰ)求证:AC⊥平面BEH;
(Ⅱ)求直线PA与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A1 , A2 , …,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为: ![]() .则下列说法中,错误的是( )
.则下列说法中,错误的是( ) 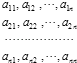
A.数阵中第一列的数全是0当且仅当A1=
B.数阵中第n列的数全是1当且仅当An=S
C.数阵中第j行的数字和表明集合Aj含有几个元素
D.数阵中所有的n2个数字之和不超过n2﹣n+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com