Question

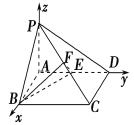
【题目】如图，在四棱锥PABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB＝2，BC＝2，E，F分别是AD，PC的中点．

(1)证明：PC⊥平面BEF；

(2)求平面BEF与平面BAP夹角的大小．

Answer 1

【答案】（1）见解析（2）45°.

【解析】

试题分析：本题主要以四棱锥为几何背景考查线线垂直、线面垂直、二面角、向量法、向量垂直的充要条件等基础知识，考查学生的空间想象能力、逻辑推理能力、计算能力.第一问，利用已知的垂直关系建立空间直角坐标系，得到点的坐标，从而得到相关向量的坐标，利用向量的数量积为0，证明两直线垂直，再利用线面垂直的判定得到PC⊥平面BEF；第二问，平面BEF与平面BAP的法向量分别为和，利用夹角公式求夹角的余弦，从而确定角的值.

试题解析：(1)证明:如图，

以A为坐标原点，AB，AD，AP所在直线分别为x，y，z轴建立空间直角坐标系．

∵AP＝AB＝2，BC＝AD＝，四边形ABCD是矩形，

∴A，B，C，D，P的坐标为A(0,0,0)，B(2,0,0)，C(2,，0)，D(0,，0)，P(0,0,2)．

又E，F分别是AD，PC的中点，∴E(0，，0)，F(1，，1)．

∴＝(2,，－2)，＝(－1，，1)，＝(1,0,1)．

∴＝－2＋4－2＝0，＝2＋0－2＝0.

∴，

∴PC⊥BF，PC⊥EF.又BF∩EF＝F，

∴PC⊥平面BEF.

(2)由(1)知平面BEF的一个法向量n1＝＝(2,，－2)，平面BAP的一个法向量n2＝＝(0,，0)，

∴n1·n2＝8.

设平面BEF与平面BAP的夹角为θ，

则，

∴θ＝45°.∴平面BEF与平面BAP的夹角为45°.