
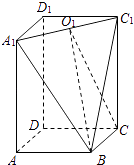
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD﹣A1C1D1 , 且这个几何体的体积为10. (Ⅰ)求棱AA1的长;
(Ⅱ)若A1C1的中点为O1 , 求异面直线BO1与A1D1所成角的余弦值.
【答案】解:(Ⅰ)设AA1=h, 由题设 ![]() =
= ![]() ﹣
﹣ ![]() =10,
=10,
∴ ![]()
即 ![]() ,解得h=3.
,解得h=3.
故A1A的长为3.
(Ⅱ)∵在长方体中,A1D1∥BC,
∴∠O1BC为异面直线BO1与A1D1所成的角(或其补角).
在△O1BC中,AB=BC=2,A1A=3,
∴AA1=BC1= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() ,
,
则cos∠O1BC= ![]() =
= ![]() =
= ![]() .
.
∴异面直线BO1与A1D1所成角的余弦值为 ![]() .
.
【解析】(Ⅰ)设AA1=h,由题设 ![]() =
= ![]() ﹣
﹣ ![]() ,可求出棱长.(Ⅱ)因为在长方体中A1D1∥BC,所以∠O1BC即为异面直线BO1与A1D1所成的角(或其补角)那么借助于三角形求解得到结论.
,可求出棱长.(Ⅱ)因为在长方体中A1D1∥BC,所以∠O1BC即为异面直线BO1与A1D1所成的角(或其补角)那么借助于三角形求解得到结论.
【考点精析】利用棱柱的结构特征和异面直线及其所成的角对题目进行判断即可得到答案,需要熟知两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形;异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:
【题目】给出以下四个结论: ①函数 ![]() 的对称中心是(﹣1,2);
的对称中心是(﹣1,2);
②若关于x的方程 ![]() 没有实数根,则k的取值范围是k≥2;
没有实数根,则k的取值范围是k≥2;
③在△ABC中,“bcosA=acosB”是“△ABC为等边三角形”的充分不必要条件;
④若 ![]() 的图象向右平移φ(φ>0)个单位后为奇函数,则φ最小值是
的图象向右平移φ(φ>0)个单位后为奇函数,则φ最小值是 ![]() .
.
其中正确的结论是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知函数f(x)=ax2﹣2x+lnx(a≠0,a∈R).
(1)判断函数 f (x)的单调性;
(2)若函数 f (x)有两个极值点x1 , x2 , 求证:f(x1)+f(x2)<﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC 的内角 A,B,C 的对边分别是a,b,c,且 ![]() a=
a= ![]() b cosC+c sinB. (Ⅰ)求角B 的大小;
b cosC+c sinB. (Ⅰ)求角B 的大小;
(Ⅱ)若点M 为BC的中点,且 AM=AC,求sin∠BAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系xoy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为  (t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ. (I)求C的直角坐标方程;
(t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ. (I)求C的直角坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA. 
(1)求证:BE⊥平面PAC;
(2)求直线AB与平面BEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行. (Ⅰ)求A;
=(cosA,sinB)平行. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=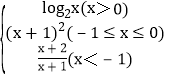 ,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com