
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取100名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在![]() 的男生人数有16人.
的男生人数有16人.
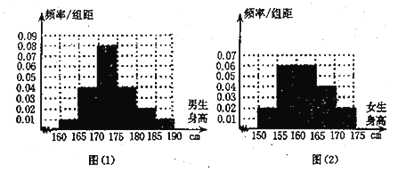
(1)试问在抽取的学生中,男,女生各有多少人?
(2)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(3)在上述100名学生中,从身高在![]() 之间的男生和身高在
之间的男生和身高在![]() 之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
参考公式:![]()
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)40,60;(2)列联表见解析,有![]() 的把握认为身高与性别有关;(3)
的把握认为身高与性别有关;(3)![]() .
.
【解析】
(1)根据直方图求出男生的人数为40,再求女生的人数;(2)完成列联表,再利用独立性检验求出有![]() 的把握认为身高与性别有关;(3)利用古典概型的概率公式求出2人中恰好有一名女生的概率.
的把握认为身高与性别有关;(3)利用古典概型的概率公式求出2人中恰好有一名女生的概率.
(1)直方图中,因为身高在![]() 的男生的频率为0.4,
的男生的频率为0.4,
设男生数为![]() ,则
,则![]() ,得
,得![]() .
.
由男生的人数为40,得女生的人数为![]() .
.
(2)男生身高![]() 的人数
的人数![]() ,
,
女生身高![]() 的人数
的人数![]() ,
,
所以可得到下列列联表:
|
| 总计 | |
男生身高 | 30 | 10 | 40 |
女生身高 | 6 | 54 | 60 |
总计 | 36 | 64 | 100 |
![]()
![]() ,
,
所以能有![]() 的把握认为身高与性别有关;
的把握认为身高与性别有关;
(3)在![]() 之间的男生有12人,在
之间的男生有12人,在![]() 之间的女生人数有6人.
之间的女生人数有6人.
按分层抽样的方法抽出6人,则男生占4人,女生占2人.
设男生为![]() ,
,![]() ,
,![]() ,
,![]() ,女生为
,女生为![]() ,
,![]() .
.
从6人任选2名有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15种可能,
共15种可能,
2人中恰好有一名女生:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8种可能,
共8种可能,
故所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集![]() 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“![]() ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量![]() ,“
,“![]() ”当且仅当“
”当且仅当“![]() ”或“
”或“![]() ”。按上述定义的关系“
”。按上述定义的关系“![]() ”,给出如下四个命题:
”,给出如下四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则对于任意
,则对于任意![]() ;
;
④对于任意向量![]() ,若
,若![]() ,则
,则![]() 。
。
其中真命题的序号为__________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
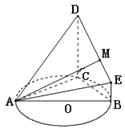
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对任意实数
满足:对任意实数![]() 以及定义中任意两数
以及定义中任意两数![]() 、
、![]() (
(![]() ),恒有
),恒有![]() ,则称
,则称![]() 是下凸函数.
是下凸函数.
(1)证明:函数![]() 是下凸函数;
是下凸函数;
(2)判断![]() 是不是下凸函数,并说明理由;
是不是下凸函数,并说明理由;
(3)若![]() 是定义在
是定义在![]() 上的下凸函数,常数
上的下凸函数,常数![]() ,满足:
,满足:![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() ,并求
,并求![]() 在
在![]() 上的解析式.
上的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)当![]() 时,判断函数
时,判断函数![]() 的单调性,并证明;
的单调性,并证明;
(3)求实教![]() 的范围,使得对于区间
的范围,使得对于区间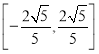 上的任意三个实数
上的任意三个实数![]() ,都存在以
,都存在以![]() 为边长的三角形.
为边长的三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. 若![]() 为假命题,则
为假命题,则![]() 均为假命题
均为假命题
C. 对于命题![]() :
:![]()
![]() ,使得
,使得![]() ,则
,则![]() :
:![]()
![]() ,均有
,均有![]()
D. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并用函数单调性的定义证明;
上的单调性,并用函数单调性的定义证明;
(3)求实数![]() 的取值范围,使得关于
的取值范围,使得关于![]() 的方程
的方程![]() 分别为:
分别为:
①有且仅有一个实数解;②有两个不同的实数解;③有三个不同的实数解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com