
【题目】某地需要修建一条大型输油管道通过720千米宽的荒漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为108万元,铺设距离为![]() 千米的相邻两增压站之间的输油管道费用为
千米的相邻两增压站之间的输油管道费用为![]() 万元.设余下工程的总费用为
万元.设余下工程的总费用为![]() 万元.
万元.
(1)试将![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(2)需要修建多少个增压站才能使总费用![]() 最小?
最小?
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,加快水污染防治,建设美丽中国.根据环保部门对某河流的每年污水排放量![]() (单位:吨)的历史统计数据,得到如下频率分布表:
(单位:吨)的历史统计数据,得到如下频率分布表:

将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(1)求在未来3年里,至多1年污水排放量![]() 的概率;(2)该河流的污水排放对沿河的经济影响如下:当
的概率;(2)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元.为减少损失,现有三种应对方案:
时,经济损失为60万元.为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费3.8万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种文案,哪种方案好,并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,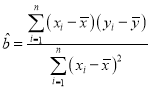
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷,某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)求出表格中![]() 的值,并根据表中的数据,判断能否在犯错误的概率不超过
的值,并根据表中的数据,判断能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.
参考公式: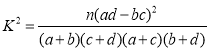 .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点Q在直线![]() 上,且
上,且![]() 。证明:过点P且垂直于OQ的直线l过C的左焦点F.
。证明:过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com