
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且在区间
上的奇函数,且在区间![]() 上单调递减,
上单调递减,![]() .设
.设![]() ,则满足
,则满足![]() 的
的![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意,由函数奇偶性的性质可得f(x)在R上为减函数以及f(﹣1)=1,结合对数函数的性质可得g(x)=log2(x+3)的定义域为(﹣3,+∞),在其定义域上,g(x)为增函数,设F(x)=f(x)﹣g(x),易得F(x)在(﹣3,+∞)上为减函数,又由F(﹣1)=f(﹣1)﹣g(﹣1)=1﹣1=0,进而可得F(x)≥0﹣3<x≤﹣1,据此分析可得答案.
根据题意,函数f(x)是定义在R上的奇函数,且在区间(﹣∞,0]上单调递减,
则f(x)在[0,+∞)上也是减函数,
则f(x)在R上为减函数,
又由f(1)=﹣1,则f(﹣1)=﹣f(1)=1,
又由g(x)=log2(x+3),有x+3>0,即x>﹣3,函数的定义域为(﹣3,+∞),在其定义域上,g(x)为增函数,
设F(x)=f(x)﹣g(x),其定义域为(﹣3,+∞),
分析易得F(x)在(﹣3,+∞)上为减函数,又由F(﹣1)=f(﹣1)﹣g(﹣1)=1﹣1=0,
F(x)≥0﹣3<x≤﹣1,
则f(x)≥g(x)F(x)≥0﹣3<x≤﹣1,即不等式的解集为(﹣3,﹣1];
故选:C.


科目:高中数学 来源: 题型:
【题目】若动点P到点F(0,1)的距离比它到直线y=﹣2的距离少1,则动点P的轨迹C的方程为_____,若过点(2,1)作该曲线C的切线l,则切线l的方程为_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4一4:坐标系与参数方程
在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心的极坐标为(
是圆心的极坐标为(![]() )且经过极点的圆
)且经过极点的圆
(1)求曲线C1的极坐标方程和C2的普通方程;
(2)已知射线![]() 分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=1,AD![]() ,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
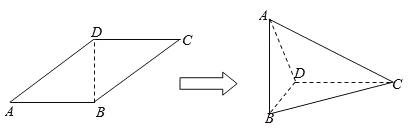
(1)求证:平面ABD⊥平面BCD;
(2)求二面角B﹣AC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一网购狂欢节”源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是
日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是![]() 月
月![]() 日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近
日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近![]() 年“双十一”期间的宣传费用
年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
(单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)建立![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),预测当宣传费用为
),预测当宣传费用为![]() 万元时的利润.
万元时的利润.
附参考公式:回归方程![]() 中
中![]() 和
和![]() 最小二乘估计公式分别为
最小二乘估计公式分别为
 ,
,![]() ,相关系数
,相关系数
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知锐角△ABC中,角A,B,C的对边分别为a,b,c,b+c=10,a=![]() ,5bsinAcosC+5csinAcosB=3a.
,5bsinAcosC+5csinAcosB=3a.
(1)求A的余弦值;
(2)求b和c.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com