
已知两同心圆的半径分别是5和4,AB为小圆的一条直径.
(1)求以大圆的切线为准线,且过A、B两点的抛物线的焦点的轨迹M;
(2)设过轨迹M的中心的弦为PQ,F是轨迹M的焦点,求S△PQF的最大值.
|
(1)建立如图所示的直角坐标系,则A(-4,0)、B(4,0),设N为大圆上的任一点,l为过N点的大圆的切线,并设抛物线的焦点为F(x,y),作AA1⊥l于A1,BB1⊥l于B1,由抛物线的定义得|AF|=|AA1|,|BF|=|BB1|.
所以|AF|+|BF|=|AA1|+|BB1|=2|OO1|=10,而A,B为定点,故焦点F的轨迹M是以A,B为焦点,长轴长为10,焦距为8的椭圆(除去长轴上的两个端点),其方程为 (2)根据椭圆的对称性,有S△PQF=2S△OFP,设△OFP的边OF上的高为h,则 S△QFP=2× 因为h≤3,所以当h=3时,S△QFP的最大面积是12. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线.若其中经过点M、N、P的双曲线的离心率分别是eM,eN,eP.则它们的大小关系是
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线.若其中经过点M、N、P的双曲线的离心率分别是eM,eN,eP.则它们的大小关系是查看答案和解析>>
科目:高中数学 来源: 题型:
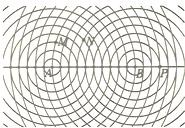 如图,已知|AB|=10,图中的一系列圆是圆心分别A,B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,利用这两组同心圆可以画出以A,B为焦点的椭圆,设其中经过点M,N,P的椭圆的离心率分别是eM,eN,eP,则( )
如图,已知|AB|=10,图中的一系列圆是圆心分别A,B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,利用这两组同心圆可以画出以A,B为焦点的椭圆,设其中经过点M,N,P的椭圆的离心率分别是eM,eN,eP,则( )| A、eM=eN=eP | B、eP<eM=eN | C、eM<eN<eP | D、eP<eM<eN |
查看答案和解析>>
科目:高中数学 来源:2013届北京市高二12月月考理科数学 题型:填空题
如图,已知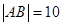 ,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是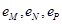 .则它们的大小关系是
(用“
.则它们的大小关系是
(用“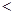 ”连接).
”连接).

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.eM=eN=eP | B.eP<eM=eN | C.eM<eN<eP | D.eP<eM<eN |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com