
【题目】在平面![]() 内,已知
内,已知![]() ,过直线
,过直线![]() ,
,![]() 分别作平面
分别作平面![]() ,
,![]() ,使锐二面角
,使锐二面角![]() 为
为![]() ,锐二面角
,锐二面角![]() 为
为![]() ,则平面
,则平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为( ).
所成的锐二面角的余弦值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
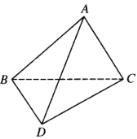
【题目】如图,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 中
中![]() ,
,![]() 沿着
沿着![]() 翻折成三棱锥
翻折成三棱锥![]() 的过程中,直线
的过程中,直线![]() 与平面
与平面![]() 所成的角均小于直线
所成的角均小于直线![]() 与平面
与平面![]() 所成的角,设二面角
所成的角,设二面角![]() ,
,![]() 的大小分别为
的大小分别为![]() ,
,![]() ,则( ).
,则( ).
A.![]() B.
B.![]()
C.存在![]() D.
D.![]() ,
,![]() 的大小关系不能确定
的大小关系不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第24届冬奥会将于2022年2月4日至2月22日在北京市和河北省张家口市联合举行,这是中国历史上第一次举办冬季奥运会.为了宣传冬奥会,让更多的人了解、喜爱冰雪项目,某校高三年级举办了冬奥会知识竞赛(总分100分),并随机抽取了![]() 名中学生的成绩,绘制成如图所示的频率分布直方图.已知前三组的频率成等差数列,第一组和第五组的频率相同.
名中学生的成绩,绘制成如图所示的频率分布直方图.已知前三组的频率成等差数列,第一组和第五组的频率相同.
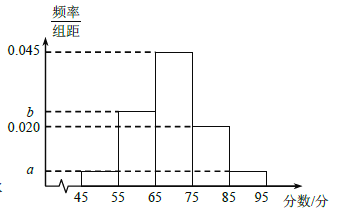
(Ⅰ)求实数![]() ,
,![]() 的值,并估计这
的值,并估计这![]() 名中学生的成绩平均值
名中学生的成绩平均值![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(Ⅱ)已知抽取的![]() 名中学生中,男女生人数相等,男生喜欢花样滑冰的人数占男生人数的
名中学生中,男女生人数相等,男生喜欢花样滑冰的人数占男生人数的![]() ,女生喜欢花样滑冰项的人数占女生人数的
,女生喜欢花样滑冰项的人数占女生人数的![]() ,且有95%的把握认为中学生喜欢花样滑冰与性别有关,求
,且有95%的把握认为中学生喜欢花样滑冰与性别有关,求![]() 的最小值.
的最小值.
参考数据及公式如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
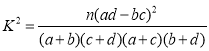 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com