
【题目】设数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
数列{an}满足a1=1,a2=4,a3=9,an=an﹣1+an﹣2﹣an﹣3(n∈N*,n≥4),即an+an﹣3=an﹣1+an﹣2(n∈N*,n≥4),a4=a3+a2﹣a1=12,同理可得:a5=17.a6=20,a7=25,a8=28,a9=33,…….可得数列{an}的奇数项与偶数项分别成等差数列,公差都为8,即可得出.
∵数列{an}满足a1=1,a2=4,a3=9,an=an﹣1+an﹣2﹣an﹣3(n∈N*,n≥4),
a4=a3+a2﹣a1=12,同理可得:a5=17.a6=20,a7=25,a8=28,a9=33,…….
有a1=1,a3=9,a5=17,a7=25,a9=33,……
a2=4,a4=12;a6=20,a8=28,……
∴数列{an}的奇数项与偶数项分别成等差数列,公差都为8.
则a2018=a2+(1009﹣1)×8=4+8064=8068.
故答案为:8068.


科目:高中数学 来源: 题型:
【题目】甲,乙,丙,丁,戊五人并排站成一排,下列说法正确的是( )
A.如果甲,乙必须相邻且乙在甲的右边,那么不同的排法有24种
B.最左端只能排甲或乙,最右端不能排甲,则不同的排法共有42种
C.甲乙不相邻的排法种数为72种
D.甲乙丙按从左到右的顺序排列的排法有20种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年入秋以来, 某市多有雾霾天气, 空气污染较为严重.市环保研究所对近期每天的空气污染情况进行调査研究后发现,每一天中空气污染指数![]() 与时刻
与时刻![]() (时)的函数关系为:
(时)的函数关系为:![]() ,其中
,其中![]() 为空气治理调节参数,且
为空气治理调节参数,且![]() .
.
(1)若![]() ,求一天中哪个时刻该市的空气污染指数最低;
,求一天中哪个时刻该市的空气污染指数最低;
(2)規定每天中![]() 的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过
的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过![]() ,则调节参数
,则调节参数![]() 应控制在什么范围内?
应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班上午有五节课,分別安排语文,数学,英语,物理,化学各一节课.要求语文与化学相邻,数学与物理不相邻,且数学课不排第一节,则不同排课法的种数是
A. 24B. 16C. 8D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是某市![]() 月
月![]() 日至
日至![]() 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(![]() )小于
)小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择![]() 月
月![]() 日至
日至![]() 月
月![]() 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留![]() 天.
天.
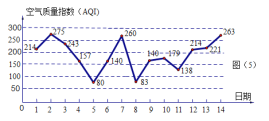
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果在一条平面曲线上存在四点,使得这四点构成的图形是一个菱形,则称该曲线存在内接菱形.现已知双曲线![]() ,双曲线
,双曲线![]() ,其中
,其中![]() ,
,![]() ,
,![]() .证明:在双曲线
.证明:在双曲线![]() 与
与![]() 中有且仅有一条存在内接菱形.
中有且仅有一条存在内接菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com