
【题目】用数学归纳法证明命题“当n是正奇数时,xn+yn能被x+y整除”,在第二步的证明时,正确的证法是( )
A.假设n=k(k∈N*)时命题成立,证明n=k+1时命题也成立
B.假设n=k(k是正奇数)时命题成立,证明n=k+1时命题也成立
C.假设n=k(k是正奇数)时命题成立,证明n=k+2时命题也成立
D.假设n=2k+1(k∈N)时命题成立,证明n=k+1时命题也成立
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1+2sinxcosx+2cos2x.
(1)求f(x)递增区间;
(2)求f(x)的对称轴方程;
(3)求f(x)的最大值并写出取最大值时自变量x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上的点到点F(0,1)的距离比它到直线y=-3的距离小2
(1)求曲线C的方程
(2)过点F且斜率为K的直线L交曲线C于A、B两点,交圆F:![]() 于M、N两点(A、M两点相邻)若
于M、N两点(A、M两点相邻)若![]()
![]()
![]() ,当
,当![]()
![]() 时,求K的取值范围
时,求K的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE. 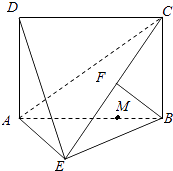
(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1+x)+lg(1﹣x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com