
分析 (1)确定从5道题中不放回地抽取2道包含的基本事件数,第1次抽到理科题的基本事件数,即可求出概率;
(2)确定第1次和第2次都抽到理科题的基本事件,即可求出概率;
(3)由已知中5道题中如果不放回地依次抽取2道题.在第一次抽到理科题的条件下,剩余4道题中,有2道理科题,代入古典概型公式,得到概率.
解答 解:一个基本事件是从5道题中不放回地抽取2道,它包含的基本事件数是A52=5×4=20.(1)设第一次抽到理科题为事件A,则它包含的基本事件的个数为A31A41=12,于是P(A)=$\frac{12}{20}$=$\frac{3}{5}$.
(2)设第1次和第2次都抽到理科题为事件B,则它包含的基本事件数为A31A21=6,于是P(B)=$\frac{6}{20}=\frac{3}{10}$.
(3)因为5道题中有3道理科题和2道文科题,所以第一次抽到理科题的前提下,第2次抽到理科题的概率为P=$\frac{2}{4}=\frac{1}{2}$.
点评 本题考查的知识点是古典概型、条件概率,分析出基本事件总数和满足条件的事件个数是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
专业 性别 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪(∁UN) | B. | ∁U(M∩N) | C. | ∁U(M∪N) | D. | (∁UM)∩N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .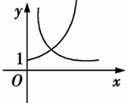 | B. | .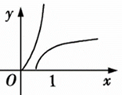 | C. | .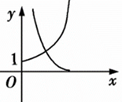 | D. | .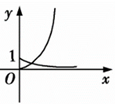 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{\overrightarrow a•\overrightarrow b}|≤|{\overrightarrow a}||{\overrightarrow b}|$ | B. | $|{\overrightarrow a-\overrightarrow b}|≤|{|{\overrightarrow a}|-|{\overrightarrow b}|}|$ | C. | ${(\overrightarrow a+\overrightarrow b)^2}={|{\overrightarrow a+\overrightarrow b}|^2}$ | D. | $(\overrightarrow a+\overrightarrow b)(\overrightarrow a-\overrightarrow b)={\overrightarrow a^2}-{\overrightarrow b^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com