
【题目】某贫困村共有农户100户,均从事水果种植,平均每户年收入为1.8万元,在当地政府大力扶持和引导下,村委会决定2020年初抽出![]() 户(
户(![]() ,
,![]() )从事水果销售工作,经测算,剩下从事水果种植的农户平均每户年收入比上一年提高了
)从事水果销售工作,经测算,剩下从事水果种植的农户平均每户年收入比上一年提高了![]() ,而从事水果销售的农户平均每户年收入为
,而从事水果销售的农户平均每户年收入为![]() 万元.
万元.
(1)为了使从事水果种植的农户三年后平均每户年收入不低于2.4万元,那么2020年初至少应抽出多少农户从事水果销售工作?
(2)若一年后,该村平均每户的年收入为![]() (万元),问
(万元),问![]() 的最大值是否可以达到2.1万元?
的最大值是否可以达到2.1万元?
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
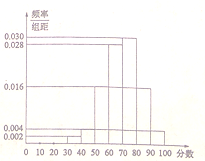
【题目】2016年某市政府出台了“2020年创建全国文明城市(简称创文)”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分, ![]() 内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
(1)求被调查者满意或非常满意该项目的频率;
(2)若从该市的全体市民中随机抽取3人,试估计恰有2人非常满意该项目的概率;
(3)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记![]() 为群众督查员中老年人的人数,求随机变量
为群众督查员中老年人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点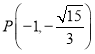 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,使得
两点,使得![]() ?若存在,求出直线的方程;若不存在,说明理由.
?若存在,求出直线的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com