
【题目】下列选项中,说法正确的是( )
A.已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假
B.命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆”
C.命题“若k<9,则方程“ ![]() +
+ ![]() =1表示双曲线”是假命题
=1表示双曲线”是假命题
D.命题“在△ABC中,若sinA< ![]() ,则A<
,则A< ![]() ”的逆否命题为真命题
”的逆否命题为真命题
【答案】B
【解析】解:对于A:若“p∨q”为假命题,则命题p和q均是假命题,故A错误;
对于B:命题“c∈R,方程2x2+y2=c表示椭圆”的否定是“c∈R,方程2x2+y2=c不表示椭圆,故B正确;
对于C:命题“若k<9,则方程“ ![]() +
+ ![]() =1表示双曲线”是真命题,故C错误;
=1表示双曲线”是真命题,故C错误;
对于D:命题“在△ABC中,若sinA< ![]() ,则A<
,则A< ![]() ”是假命题,故其逆否命题为假命题,故D错误;
”是假命题,故其逆否命题为假命题,故D错误;
故选:B.
【考点精析】利用四种命题的真假关系对题目进行判断即可得到答案,需要熟知一个命题的真假与其他三个命题的真假有如下三条关系:(原命题 逆否命题)①、原命题为真,它的逆命题不一定为真;②、原命题为真,它的否命题不一定为真;③、原命题为真,它的逆否命题一定为真.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(﹣π<φ<0,ω>0)的图象关于直线 ![]() 对称,且两相邻对称中心之间的距离为
对称,且两相邻对称中心之间的距离为 ![]() .
.
(1)求函数y=f(x)的单调递增区间;
(2)若关于x的方程f(x)+log2k=0在区间 ![]() 上总有实数解,求实数k的取值范围.
上总有实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* .
(1)证明:数列{ ![]() }是等差数列;
}是等差数列;
(2)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点,且PA=AD. 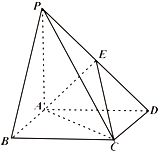
(1)求证:PB∥平面AEC;
(2)求证:AE⊥平面PCD;
(3)设二面角D﹣AE﹣C为60°,且AP=1,求D到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点 
(1)求证:DE∥平面ABC;
(2)求三棱锥E﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (p﹣2)x2+(2q﹣8)x+1(p>2,q>0).
(p﹣2)x2+(2q﹣8)x+1(p>2,q>0).
(1)当p=q=3时,求使f(x)≥1的x的取值范围;
(2)若f(x)在区间[ ![]() ,2]上单调递减,求pq的最大值.
,2]上单调递减,求pq的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8, 
(1)求频率分布直方图中a,b的值;
(2)根据频率分布直方图,估计这20棵果树产量的中位数;
(3)根据频率分布直方图,估计这1000棵果树的总产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( ) 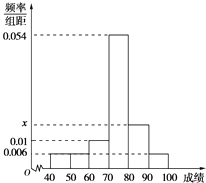
A.75.5
B.75.2
C.75.1
D.75.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com