
在2000年至2003年期间,甲每年6月1日都到银行存入 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为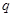 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
A.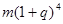 元 元 | B.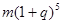 元 元 |
C.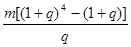 元 元 | D. 元 元 |
科目:高中数学 来源: 题型:单选题
在数列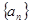 中,如果存在常数
中,如果存在常数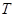
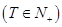 ,使得
,使得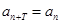 对于任意正整数
对于任意正整数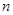 均成立,那么就称数列
均成立,那么就称数列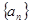 为周期数列,其中
为周期数列,其中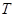 叫做数列
叫做数列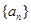 的周期. 已知数列
的周期. 已知数列 满足
满足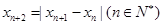 ,若
,若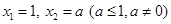 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和
的前2012项的和 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数: 1,1,2,3,5,8,13,其中从第三个数起,每一个数都等于他前而两个数的和.该数列是一个非常美丽、和谐的数列,有很多奇妙的属性.比如:随着数列项数的增加,前一项与后一项之比越逼近黄金分割0.6180339887 .人们称该数列{an}为“斐波那契数列”.若把该数列{an}的每一项除以4所得的余数按相对应的顺序组成新数列{bn},在数列{bn}中第2014项的值是_______]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com