
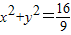 ,直线l:x+3y-8=0,若点A∈l,使得⊙O上存在点B满足∠OAB=30°(O为坐标原点),则点A的横坐标的取值范围是 .
,直线l:x+3y-8=0,若点A∈l,使得⊙O上存在点B满足∠OAB=30°(O为坐标原点),则点A的横坐标的取值范围是 .  的点的横坐标即可.
的点的横坐标即可.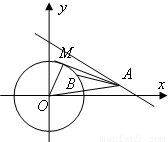 解:设点A(x,y)如图,当∠OAB=30°时,连接OB,就得到一个∠OAB=30°的三角形,这时OA=2OB,圆O的半径是
解:设点A(x,y)如图,当∠OAB=30°时,连接OB,就得到一个∠OAB=30°的三角形,这时OA=2OB,圆O的半径是 ,那么只要求出在直线I上距圆心为
,那么只要求出在直线I上距圆心为 的点的横坐标,就是所求范围,
的点的横坐标,就是所求范围,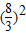 与 x+3y-8=0
与 x+3y-8=0 .
. ]
]

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
|
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
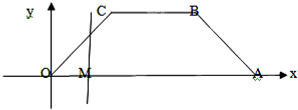 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.| 7 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知m>1,直线l:x-my-
已知m>1,直线l:x-my-| m |
| 2 |
| x2 |
| m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
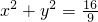 ,直线l:x+3y-8=0,若点A∈l,使得⊙O上存在点B满足∠OAB=30°(O为坐标原点),则点A的横坐标的取值范围是________.
,直线l:x+3y-8=0,若点A∈l,使得⊙O上存在点B满足∠OAB=30°(O为坐标原点),则点A的横坐标的取值范围是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com