
【题目】已知向量 ![]() =(2cosx,sinx),
=(2cosx,sinx), ![]() =(cosx,2
=(cosx,2 ![]() cosx),函数f(x)=
cosx),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在锐角△ABC中,内角A、B、C的对边分别为a,b,c,tanB= ![]() ,对任意满足条件的A,求f(A)的取值范围.
,对任意满足条件的A,求f(A)的取值范围.
【答案】解:(Ⅰ)向量 ![]() =(2cosx,sinx),
=(2cosx,sinx), ![]() =(cosx,2
=(cosx,2 ![]() cosx),
cosx),
函数f(x)= ![]()
![]() ﹣1.
﹣1.
则f(x)=2cos2x+2 ![]() sinxcosx﹣1=
sinxcosx﹣1= ![]() sin2x+cos2x=2sin(2x
sin2x+cos2x=2sin(2x ![]() )
)
由 ![]() ,
,
解得: ![]() ≤x≤
≤x≤ ![]() ,(k∈Z).
,(k∈Z).
故得函数f(x)的单调递减区间为[ ![]() ,
, ![]() ],(k∈Z)
],(k∈Z)
(Ⅱ)由tanB= ![]() ,即:
,即: ![]() ,
,
∵cosB= ![]()
∴sinB= ![]() .
.
又∵△ABC是锐角,
∴B= ![]() .
.
则 ![]() <A<
<A< ![]()
由(Ⅰ)可知f(A)=2sin(2A ![]() )
)
那么:2A ![]() ∈(
∈( ![]() ,
, ![]() )
)
则sin(2A ![]() )∈(
)∈( ![]() ,1)
,1)
故得f(A)的取值范围是(﹣1,2)
【解析】(Ⅰ)根据函数f(x)= ![]()
![]() ﹣1.利用向量的数量积的运算求解f(x),结合三角函数的性质求解单调性即可.(Ⅱ)tanB=
﹣1.利用向量的数量积的运算求解f(x),结合三角函数的性质求解单调性即可.(Ⅱ)tanB= ![]() 求解.
求解.
【考点精析】掌握余弦定理的定义是解答本题的根本,需要知道余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量 ![]() =[
=[ ![]() ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,若不等式f(x)≤3的解集为{|x|﹣1≤x≤5}. (Ⅰ)求实数a的值:
(Ⅱ)若不等式f(3x)+f(x+3)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌的汽车4S店,对最近100例分期付款购车情况进行统计,统计结果如表所示,已知分9期付款的频率为0.4;该店经销一辆该品牌的汽车.若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 | a | b |
(1)若以表中计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3位顾客,求事件A:“至多有1位采用分6期付款”的概率P(A);
(2)按分层抽样的方式从这100位顾客中抽出5人,再从抽出的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量η,求η的分布列及数学期望E(η).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( ) 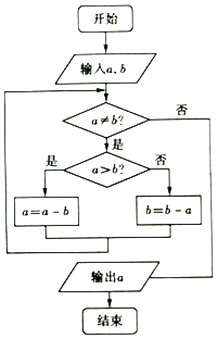
A.14
B.7
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为 ![]() (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,与直角坐标系xoy取相同的单位长度建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ.
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,与直角坐标系xoy取相同的单位长度建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ.
(1)化曲线C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C2与x轴的一个交点的坐标为P(m,0)(m>0),经过点P作斜率为1的直线,l交曲线C2于A,B两点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}和{bn}中,a1= ![]() ,{an}的前n项为Sn , 满足Sn+1+(
,{an}的前n项为Sn , 满足Sn+1+( ![]() )n+1=Sn+(
)n+1=Sn+( ![]() )n(n∈N*),bn=(2n+1)an , {bn}的前n项和为Tn .
)n(n∈N*),bn=(2n+1)an , {bn}的前n项和为Tn .
(1)求数列{bn}的通项公式bn以及Tn .
(2)若T1+T3 , mT2 , 3(T2+T3)成等差数列,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1的图象向左平移
cos2x+1的图象向左平移 ![]() 个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
A.函数y=g(x)的最小正周期为π
B.函数y=g(x)的图象的一条对称轴为直线x= ![]()
C.![]() g(x)dx=
g(x)dx= ![]()
D.函数y=g(x)在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已成椭圆C: ![]() =1(a>b>0)的左右顶点分别为A1、A2 , 上下顶点分别为B2/B1 , 左右焦点分别为F1、F2 , 其中长轴长为4,且圆O:x2+y2=
=1(a>b>0)的左右顶点分别为A1、A2 , 上下顶点分别为B2/B1 , 左右焦点分别为F1、F2 , 其中长轴长为4,且圆O:x2+y2= ![]() 为菱形A1B1A2B2的内切圆.
为菱形A1B1A2B2的内切圆.
(1)求椭圆C的方程;
(2)点N(n,0)为x轴正半轴上一点,过点N作椭圆C的切线l,记右焦点F2在l上的射影为H,若△F1HN的面积不小于 ![]() n2 , 求n的取值范围.
n2 , 求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com