
【题目】已知平面上一动点P到定点C(1,0)的距离与它到直线![]() 的距离之比为
的距离之比为![]() .
.
(1)求点P的轨迹方程;
(2)点O是坐标原点,A,B两点在点P的轨迹上,F是点C关于原点的对称点,若![]() ,求
,求![]() 的取值范围.
的取值范围.
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥P-ABC中,顶点P在底面ABC的投影G是ABC的外心,PB=BC=2,则面PBC与底面ABC所成的二面角的大小为60,则三棱锥PABC的外接球的表面积为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区![]() 年该农产品的产量;
年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 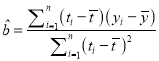 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在底面为梯形的四棱锥S﹣ABCD中,已知AD∥BC,∠ASC=60°,![]() ,SA=SC=SD=2.
,SA=SC=SD=2.
(1)求证:AC⊥SD;
(2)求三棱锥B﹣SAD的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台“挑战主持人”节目的挑战者闯第一关需要回答三个问题,其中前两个问题回答正确各得![]() 分,回答不正确得
分,回答不正确得![]() 分,第三个问题回答正确得
分,第三个问题回答正确得![]() 分,回答不正确得
分,回答不正确得![]() 分.如果一个挑战者回答前两个问题正确的概率都是
分.如果一个挑战者回答前两个问题正确的概率都是![]() ,回答第三个问题正确的概率为
,回答第三个问题正确的概率为![]() ,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题总分不低于
,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题总分不低于![]() 分就算闯关成功.
分就算闯关成功.
(Ⅰ)求至少回答对一个问题的概率;
(Ⅱ)求这位挑战者回答这三个问题的总得分X的分布列;
(Ⅲ)求这位挑战者闯关成功的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取100名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在![]() 的男生人数有16人.
的男生人数有16人.
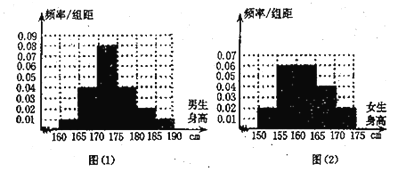
(1)试问在抽取的学生中,男,女生各有多少人?
(2)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(3)在上述100名学生中,从身高在![]() 之间的男生和身高在
之间的男生和身高在![]() 之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
参考公式:![]()
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 经过点
经过点![]() ,且点
,且点![]() 为其一个焦点.
为其一个焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 与
与![]() 轴的两个交点为
轴的两个交点为![]() ,
,![]() ,不在
,不在![]() 轴上的动点
轴上的动点![]() 在直线
在直线![]() 上运动,直线
上运动,直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() ,证明:直线
,证明:直线![]() 通过一个定点,且
通过一个定点,且![]() 的周长为定值.
的周长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com