
分析 (1)设出A、B坐标,利用斜率公式及直线PA与PB的倾斜角互补两直线斜率相反,从而求出AB斜率.
(2)若PA⊥PB,则两直线斜率积为-1,求出直线AB 的方程,可得直线AB经过定点(-2,5).
解答 证明:(1)设点A(x1,$\frac{{{x}_{1}}^{2}}{4}$),B(x2,$\frac{{{x}_{2}}^{2}}{4}$),
若直线PA与PB的倾斜角互补,则两直线斜率相反,
又kPA=$\frac{\frac{{{x}_{1}}^{2}}{4}-1}{{x}_{1}-2}$=$\frac{{x}_{1}+2}{4}$,kPB=$\frac{\frac{{{x}_{2}}^{2}}{4}-1}{{x}_{2}-2}$=$\frac{{x}_{2}+2}{4}$,
所以$\frac{{x}_{1}+2}{4}$+$\frac{{x}_{2}+2}{4}$=0,
整理得x1+x2+4=0,
所以kAB=$\frac{\frac{{{x}_{1}}^{2}}{4}-\frac{{{x}_{2}}^{2}}{4}}{{x}_{1}-{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{4}$=-1.
(2)解:因为PA⊥PB,
所以kPAkPB=$\frac{{x}_{1}+2}{4}$•$\frac{{x}_{2}+2}{4}$=-1,
即x1x2+2(x1+x2)+20=0,①
直线AB的方程为:$\frac{\frac{{{x}_{1}}^{2}}{4}-y}{\frac{{{x}_{1}}^{2}}{4}-\frac{{{x}_{2}}^{2}}{4}}=\frac{{x}_{1}-x}{{x}_{1}-{x}_{2}}$,
整理得:4y-${{x}_{1}}^{2}$=(x1+x2)(x-x1),
即x1x2-x(x1+x2)+4y=0,②
由①②可得$\left\{\begin{array}{l}-x=2\\ 4y=20\end{array}\right.$,
解得$\left\{\begin{array}{l}x=-2\\ y=5\end{array}\right.$,
即直线AB经过定点(-2,5).
点评 本题考查的知识点是直线与抛物线的位置关系,直线过定点问题,斜率公式,难度中档.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
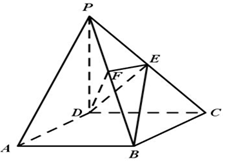 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC中点,作EF⊥PB,交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC中点,作EF⊥PB,交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1<x3<x2 | B. | x2<x1<x3 | C. | x1<x2<x3 | D. | x3<x1<x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要而不充分条件 | ||
| C. | 充分而不必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | $({\frac{1}{2},+∞})$ | C. | (1,+∞) | D. | (e,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com