Question

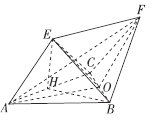
【题目】如图所示，在多面体中，是边长为2的等边三角形，为的中点，．

（1）若平面平面，证明：；

（2）求证：；

（3）若，求点到平面的距离．

Answer 1

【答案】（1）详见解析（2）详见解析（3）

【解析】

试题分析：（1）证明线线平行，一般利用线面平行性质定理，即先证明线面平行：平面，而证明线面平行，就要利用线面平行判定定理，即从线线平行出发：由得平面，（2）证明线线垂直，一般利用线面垂直给予证明，即由等边三角形与等腰三角形性质得，，（为的中点），确定线面垂直平面，即得（3）求点到平面的距离，一般利用等体积法，即将点到面的距离转化为高：

试题解析：（1）因为平面平面，

所以平面，

又因为平面平面，所以

（2）取的中点，连接，因为，所以，

因为为等边三角形，所以，

因为，所以平面，

因为平面，所以

（3）

因为在中，，

所以，

因为为等边三角形，所以，

因为，所以，所以，

因为，所以平面，

又因为，所以，

因为，所以,

因为，四边形为平行四边形，，

所以，

设点到平面的距离为，

由，得，解得