
已知函数f(x)=ax- -3ln x,其中a为常数.
-3ln x,其中a为常数.
(1)当函数f(x)的图象在点 处的切线的斜率为1时,求函数f(x)在
处的切线的斜率为1时,求函数f(x)在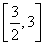 上的最小值;
上的最小值;
(2)若函数f(x)在区间(0,+∞)上既有极大值又有极小值,求a的取值范围;
(3)在(1)的条件下,过点P(1,-4)作函数F(x)=x2[f(x)+3lnx-3]图象的切线,试问这样的切线有几条?并求出这些切线方程.
(1) 1-3ln 2 (2) 0<a<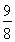 (3) 满足条件的切线只有一条,其方程为5x+y-1=0.
(3) 满足条件的切线只有一条,其方程为5x+y-1=0.
【解析】
解:(1)由题可知f′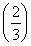 =1,解得a=1,
=1,解得a=1,
故f(x)=x-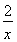 -3ln x,∴f′(x)=
-3ln x,∴f′(x)=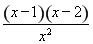 ,
,
由f′(x)=0得x=2或x=1.
于是可得x∈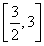 的下表:
的下表:
|
| 2 | (2,3] |
f′(x) | - | 0 | + |
f(x) | ↘ | 1-3ln 2 | ↗ |
于是可得f(x)min=f(2)=1-3ln 2.
(2)∵f′(x)=a+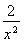 -
-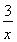 =
=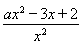 (x>0),
(x>0),
由题可得方程ax2-3x+2=0有两个不等的正实根,不妨设这两个根为x1、x2,
则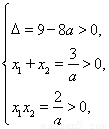
解得0<a<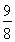 .
.
(3)由(1)f(x)=x-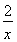 -3ln x,
-3ln x,
故F(x)=x3-3x2-2x(x>0),F′(x)=3x2-6x-2(x>0).
设切点为T(x0,y0),由于点P在函数F(x)的图象上,
①当切点T不与点P(1,-4)重合,即当x0≠1时,由于切线过点P(1,-4),则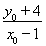 =3
=3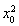 -6x0-2,
-6x0-2,
所以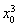 -3
-3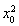 -2x0+4=(x0-1)(3
-2x0+4=(x0-1)(3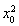 -6x0-2),
-6x0-2),
化简得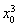 -3
-3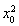 +3x0-1=0,即(x0-1)3=0,
+3x0-1=0,即(x0-1)3=0,
解得x0=1(舍去).
②当切点T与点P(1,-4)重合,即x0=1时,
则切线的斜率k=F′(1)=-5,
于是切线方程为5x+y-1=0.
综上所述,满足条件的切线只有一条,
其方程为5x+y-1=0.


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
| 1 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x-1) | x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com