
【题目】某学校为培养学生的兴趣爱好,提高学生的综合素养,在高一年级开设各种形式的校本课程供学生选择(如书法讲座、诗歌鉴赏、奥赛讲座等).现统计了某班50名学生一周用在兴趣爱好方面的学习时间(单位:h)的数据,按照[0,2),[2,4),[4,6),[6,8),[8,10]分成五组,得到了如下的频率分布直方图.
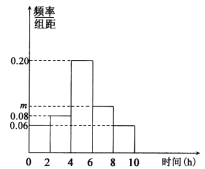
(1)求频率分布直方图中m的值及该班学生一周用在兴趣爱好方面的平均学习时间;
(2)从[4,6),[6,8)两组中按分层抽样的方法抽取6人,再从这6人中抽取2人,求恰有1人在[6,8)组中的概率.
【答案】(1)m=0.1,平均时间为5.08;(2)![]()
【解析】
(1)首先根据概率之和为1即可计算出![]() 的值,然后通过计算每一组的概率乘时间并求和即可计算出平均学习时间;
的值,然后通过计算每一组的概率乘时间并求和即可计算出平均学习时间;
(2)本题首先可以通过分层抽样的相关性质来确定![]() 以及
以及![]() 两组中所抽取的人数,然后写出从6人中抽取2人的所有可能事件以及恰有一人在
两组中所抽取的人数,然后写出从6人中抽取2人的所有可能事件以及恰有一人在![]() 组中的所有可能事件,两者相除,即可得出结果。
组中的所有可能事件,两者相除,即可得出结果。
(l)由直方图可得:![]() ,所以
,所以![]() ,
,
学生的平均学习时间:![]() ;
;
(2)由直方图可得:![]() 中有
中有![]() 人,
人,![]() 中有
中有![]() 人,
人,
根据分层抽样,需要从![]() 中抽取
中抽取![]() 人分别记为
人分别记为![]() ,
,
从![]() 中抽取
中抽取![]() 人分别记为
人分别记为![]() ,
,
再从这![]() 人中抽取
人中抽取![]() 人,所有的抽取方法有
人,所有的抽取方法有![]()
![]() 共15种,
共15种,
其中恰有一人在![]() 组中的抽取方法有
组中的抽取方法有![]()
![]() 共8种,
共8种,
所以,从这![]() 人中抽取
人中抽取![]() 人,恰有
人,恰有![]() 人在
人在![]() 组中的概率为
组中的概率为![]() 。
。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,且∠DAB=60°.点E是棱PC的中点,平面ABE与棱PD交于点F.
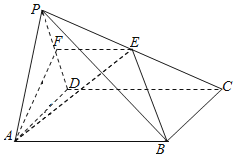
(1)求证:AB∥EF;
(2)若PA=PD=AD,且平面PAD⊥平面ABCD,求平面PAF与平面AFE所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
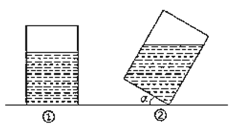
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
, ![]() ,点
,点![]() 满足:
满足: ![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
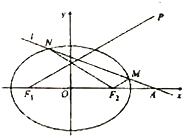
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若斜率为![]() (
(![]() )的直线
)的直线![]() 与
与![]() 轴、椭圆
轴、椭圆![]() 顺次相交于点
顺次相交于点![]() 、
、![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销量y(元) | 88 | 78 | 85 | 75 | 82 | 66 |
(1)分别以三家连锁店的平均售价与平均销量为散点,如A店对应的散点为![]() ,求出售价与销量的回归直线方程
,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附: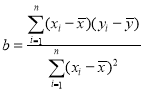 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
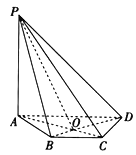
(1)证明:BD⊥PC;
(2)若AD=4,BC=2,设AC∩BD=O,且∠PDO=60°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知双曲线与椭圆![]() 有相同焦点,且过点
有相同焦点,且过点![]() ,求双曲线标准方程;
,求双曲线标准方程;
(2)已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,椭圆上一点
,椭圆上一点![]() 到焦点
到焦点![]() 的最大距离是3,求这个椭圆的离心率.
的最大距离是3,求这个椭圆的离心率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com