
【题目】从8名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?(用数字结尾)
(1)甲、乙两人必须跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒.
【答案】(1)60; (2)480;(3)180.
【解析】
(1)甲、乙两人必须跑中间两棒,甲和乙两个人本身有一个排列,余下的两个位置需要在6个人中选个排列;(2)甲、乙两人只有一人被选且不能跑中间两棒,需要从甲和乙两个人中选出一个有![]() 种结果,需要在第一和第四棒中选一棒,有
种结果,需要在第一和第四棒中选一棒,有![]() 种结果,另外6个人要选三个在三个位置排列;(3)首先甲和乙两个人在相邻的位置本身有
种结果,另外6个人要选三个在三个位置排列;(3)首先甲和乙两个人在相邻的位置本身有![]() 种结果,其余6名同学选两人三个元素在三个位置排列共有
种结果,其余6名同学选两人三个元素在三个位置排列共有![]() 种结果,根据计数原理得到结果.
种结果,根据计数原理得到结果.
(1)甲、乙两人必须跑中间两棒,甲和乙两个人本身有一个排列,
余下的两个位置需要在6个人中选2个排列
根据分步计数原理知道共有![]() ;
;
(2)甲、乙两人只有一人被选且不能跑中间两棒,
需要从甲和乙两个人中选出一个有![]() 种结果,
种结果,
需要在第一和第四棒中选一棒,有![]() 种结果,
种结果,
另外6个人要选三个在三个位置排列,根据计数原理共有![]() ;
;
(3)∵甲、乙两名同学必须入选,而且必须跑相邻两棒
∴首先甲和乙两个人在相邻的位置本身有![]() 种结果,
种结果,
其余6名同学选两人三个元素在三个位置排列共有![]() 种结果,
种结果,
根据分步计数原理得到共有![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b
(a,b![]() R).
R).
(1)当a=b=1时,求![]() 的单调增区间;
的单调增区间;
(2)当a≠0时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当a=0时,若![]() 的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把![]() ,
,![]() ,
,![]() ,
,![]() 四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,
四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,![]() ,
,![]() 不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义域为
定义域为![]() ,设
,设![]() .
.
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(2)求证:![]() ;
;
(3)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,并确定这样的
,并确定这样的![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求证:x1+x2<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种细菌的繁殖个数y随天数x的变化情况,收集数据如下:
天数x | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
(1)根据散点图,判断![]() 与
与![]() 哪一个适合作为y关于x的回归方程类型;(给出判断即可,不用说明理由)
哪一个适合作为y关于x的回归方程类型;(给出判断即可,不用说明理由)
(2)根据(1)中的判断及表中数据,求y关于x的回归方程![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: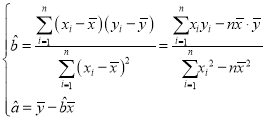
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com