[题目]已知A.B.C.D为圆O上的四点.直线DE为圆O的切线.AC∥DE.AC与BD相交于H点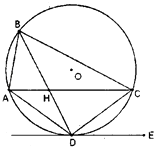．(1)求证:BD平分∠ABC,(2)若AB=4.AD=6.BD=8.求AH的长．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知A、B、C、D为圆O上的四点，直线DE为圆O的切线，AC∥DE，AC与BD相交于H点．

（1）求证：BD平分∠ABC；
（2）若AB=4，AD=6，BD=8，求AH的长．

【答案】
（1）

解：∵AC∥DE，直线DE为圆O的切线，∴D是弧的中点，即

又∠ABD，∠DBC与分别是两弧所对的圆周角，故有∠ABD=∠DBC，

所以BD平分∠ABC

（2）

解：∵由图∠CAB=∠CDB且∠ABD=∠DBC

∴△ABH∽△DBC，∴

又

∴AD=DC，

∴

∵AB=4，AD=6，BD=8

∴AH=3

【解析】（1）证明BD平分∠ABC可通过证明D是的中点，利用相等的弧所对的圆周角相等证明BD是角平分线；（2）由图形知，可先证△ABH∽△DBC，得到，再由等弧所对的弦相等，得到AD=DC，从而得到，求出AH的长

练习册系列答案

一通百通小学毕业升学模拟测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设函数 (为自然对数的底数），.

（1）证明：当时，没有零点；

（2）若当时，恒成立，求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】海南大学某餐饮中心为了解新生的饮食习惯，在全校新生中进行了抽样调查，调查结果如下表所示：

	喜欢甜品	不喜欢甜品	合计
南方学生	60	20	80
北方学生	10	10	20
合计	70	30	100

(Ⅰ)根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；

(Ⅱ)已知在被调查的北方学生中有5名中文系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率．

附：，K2＝

P(K2≥k0)	0.10	0.05	0.010
k0	2.706	3.841	6.635

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设数列{an}的前n项和为Sn ，若对任意的正整数n，总存在正整数m，使得Sn=am ，则称{an}是“H数列”．
（1）若数列{an}的前n项和为Sn=2n（n∈N*），证明：{an}是“H数列”；
（2）设{an}是等差数列，其首项a1=1，公差d＜0，若{an}是“H数列”，求d的值；
（3）证明：对任意的等差数列{an}，总存在两个“H数列”{bn}和{cn}，使得an=bn+cn（n∈N*）成立．