
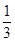 +
+ =1;
=1;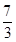 +
+ +
+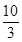 +
+ =12;
=12;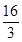 +
+ +
+ +
+ +
+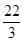 +
+ =39;
=39; +
+ +
+ +
+ +…+
+…+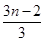 +
+ =________(最后结果用m,n表示).
=________(最后结果用m,n表示).科目:高中数学 来源:不详 题型:填空题
 +2=4;
+2=4; ×2=4;
×2=4; +3=
+3= ;
; ×3=
×3= ;
; +4=
+4= ;
; ×4=
×4= ;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若a与b共线,则a☉b=0 |
| B.a☉b=b☉a |
| C.对任意的λ∈R,有(λa)☉b=λ(a☉b) |
| D.(a☉b)2+(a·b)2=|a|2|b|2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 个图形包含的小圆圈个数为
个图形包含的小圆圈个数为 ,则(Ⅰ)
,则(Ⅰ) = ;(Ⅱ)
= ;(Ⅱ) 的个位数字为 .
的个位数字为 .
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com