已知函数

.
(Ⅰ)若函数

的值域为

.求关于

的不等式

的解集;
(Ⅱ)当

时,

为常数,且
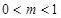
,
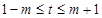
,求

的最小值.
(Ⅰ)
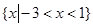
;(Ⅱ)
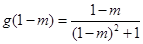
.
试题分析:(Ⅰ)由函数

的值域为

,则该二次函数与

轴有一个交点,即
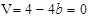
,所以
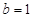
,所以
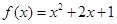
,则
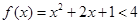
,则
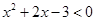
,化简得
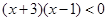
,解得
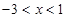
,所以不等式的解集为
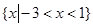
.(Ⅱ)当

时,
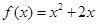
,所以
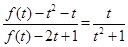
,而
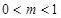
,
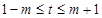
,所以
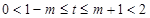
,接着利用导数求
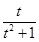
的最小值,令
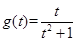
,则
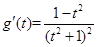
,当
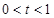
时,
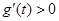
,
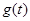
单调增,当
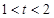
时,
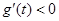
,
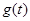
单调减,最小值需要比较
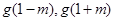
的大小,而
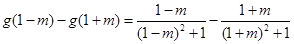
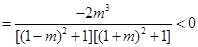
,
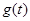
的最小值为
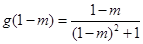
.
试题解析:(Ⅰ)由值域为
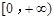
,当
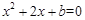
时有
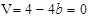
,即
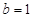
,
所以
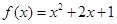
,则
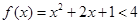
则
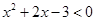
,化简得
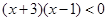
,解得
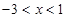
所以不等式的解集为
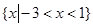
.
(Ⅱ)当

时,
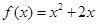
,所以
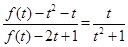
因为
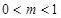
,
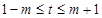
,所以
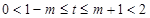
令
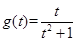
,则
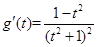
当
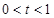
时,
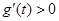
,
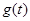
单调增,当
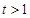
时,
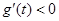
,
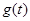
单调减,
因为
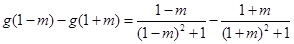
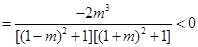
,所以
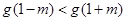
所以
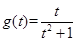
的最小值为
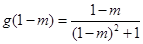
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
设函数
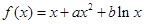
,其对应的图像为曲线C;若曲线C过
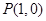
,且在
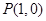
点处的切斜线率
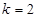
(1)求函数
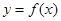
的解析式
(2)证明不等式
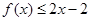
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
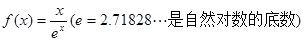
.
(1)求
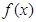
的单调区间及最大值;
(2)
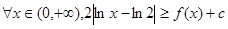
恒成立,试求实数
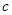
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
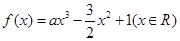
,其中
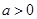
.
(1)若
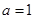
,求曲线
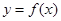
在点
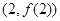
处的切线方程;
(2)求函数的极大值和极小值,若函数
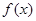
有三个零点,求
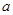
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
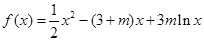
,
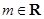
.
(Ⅰ)求函数
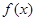
的单调递增区间;
(Ⅱ)设
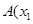
,
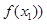
,
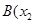
,
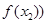
为函数
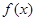
的图象上任意不同两点,若过
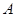
,
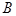
两点的直线
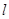
的斜率恒大于
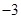
,求
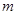
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
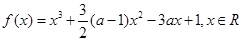
.
(Ⅰ)讨论函数

的单调区间;
(Ⅱ)当
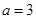
时,若函数

在区间
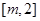
上的最大值为28,求

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
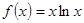
,若
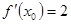
,则x
0等于 ( )
查看答案和解析>>

 .
. 的值域为
的值域为 .求关于
.求关于 的不等式
的不等式 的解集;
的解集; 时,
时, 为常数,且
为常数,且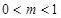 ,
,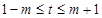 ,求
,求 的最小值.
的最小值.