
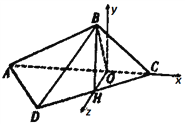
【题目】如图甲,已知矩形![]() 中,
中, ![]() 为
为![]() 上一点,且
上一点,且![]() ,垂足为
,垂足为![]() ,现将矩形
,现将矩形![]() 沿对角线
沿对角线![]() 折起,得到如图乙所示的三棱锥
折起,得到如图乙所示的三棱锥![]() .
.

(Ⅰ)在图乙中,若![]() ,求
,求![]() 的长度;
的长度;
(Ⅱ)当二面角![]() 等于
等于![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() (2)余弦值为
(2)余弦值为![]() .
.
【解析】试题分析:(Ⅰ)当![]() 时,由线面垂直的判定定理,可得
时,由线面垂直的判定定理,可得![]() 平面
平面![]() ,所以
,所以![]() ,由勾股定理求出BH的长度;(Ⅱ)以
,由勾股定理求出BH的长度;(Ⅱ)以![]() 为坐标原点,
为坐标原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,垂直于平面
轴,垂直于平面![]() 的方向为
的方向为![]() 轴建系,可得平面ADC的法向量为
轴建系,可得平面ADC的法向量为![]() ,由当二面角
,由当二面角![]() 等于
等于![]() ,求出点B,C,H三点的坐标,假设平面
,求出点B,C,H三点的坐标,假设平面![]() 的法向量
的法向量![]() ,由
,由![]() ,求出
,求出![]() ,根据两向量的夹角公式,求出二面角
,根据两向量的夹角公式,求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)由![]() ,可得折叠后
,可得折叠后![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
解得![]() ,
, ![]() ,由勾股定理,
,由勾股定理,
![]() .
.
(Ⅱ)如图,以![]() 为坐标原点,
为坐标原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,垂直于平面
轴,垂直于平面![]() 的方向为
的方向为![]() 轴建系,
轴建系,
可得平面![]() 的法向量为
的法向量为![]() ,
,
即有![]() ,再由二面角
,再由二面角![]() 等于
等于![]() ,
,
可得![]() 点坐标为
点坐标为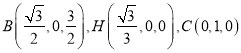 ,
,
所以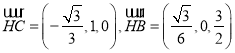 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则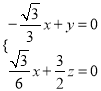
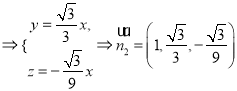 ,
,
所以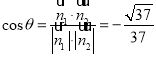 ,
,
由横坐标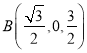 大于
大于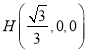 横坐标,
横坐标,
所以二面角![]() 为钝角,所以余弦值为
为钝角,所以余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+2(a﹣1)x+2在区间[﹣1,2]上单调,则实数a的取值范围为( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 届高三文(1)班在一次数学测验中,全班
届高三文(1)班在一次数学测验中,全班![]() 名学生的数学成绩的频率分布直方图如下,已知分数在
名学生的数学成绩的频率分布直方图如下,已知分数在![]() 的学生数有
的学生数有![]() 人.
人.
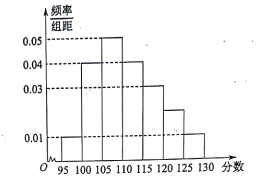
(1)求总人数![]() 和分数在
和分数在![]() 的人数
的人数![]() ;
;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现在从比分数在![]() 名学生(男女生比例为
名学生(男女生比例为![]() )中任选
)中任选![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com