
【题目】(本小题满分12分)
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5.同时投掷这两枚玩具一次,记![]() 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(Ⅰ)求事件“m不小于6”的概率;
(Ⅱ)“m为奇数”的概率和“m为偶数”的概率是不是相等?证明你作出的结论.
【答案】解:(1)因玩具是均匀的,所以玩具各面朝下的可能性相等,出现的可能情况有
(1,1),(1,2),(1,3),(1,5),(2,1),(2,2),(2,3),(2,5)
(3,1),(3,2),(3,3),(3,5),(5,1),(5,2),(5,3),(5,5)
共16种 4分
(1)事件“m不小于6”包含其中(1,5),(2,5),(3,5),(3,3)(5,1),(5,2),(5,
3),(5,8)共8个基本事件 6分
所以P(m≥6)=![]() 8分
8分
(2)“m为奇数”的概率和“m为偶数”的概率不相等。
因为m为奇数的概率为![]() 11分
11分
M为偶数的概率为![]() 。这两个概率值不相等 13分
。这两个概率值不相等 13分
【解析】
本试题主要是考查了古典概型的概率的 运算,先分析总的试验空间 然后分析事件A发生基本事件书,利用古典概型的概率公式可以解得。
解:因玩具是均匀的,所以玩具各面朝下的可能性相等,出现的可能性有16种。
(1) 事件“m不小于6”包含(1,5),(2,5),(3,5),(3,3),(5,1),(5,2),(5,3),(5,5)共8个基本事件。
所以p(m≤6)= 8/16=1/2
(2) “m为奇数”的概率和“m为偶数”的概率不相等。
“m为奇数”的概率为p(m=3)+ p(m=5)+ p(m=7)=2/16+2/16+2/16=3/8
“m为偶数”的概率为1-3/8=5/8.这两个概率值不相等。


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区10名健康儿童头发和血液中的硒含量(单位:μg/ml)如下表所示:
血硒x | 74 | 66 | 88 | 69 | 91 | 73 | 66 | 96 | 58 | 73 |
发硒y | 13 | 10 | 13 | 11 | 16 | 9 | 7 | 14 | 5 | 10 |
(1)画出散点图;
(2)求回归方程;
(3)若某名健康儿童的血液中的硒含量为94 μg/ml,预测他的发硒含量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (其中
(其中![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 作曲线
作曲线![]() 的切线交圆
的切线交圆![]() 于不同的两点
于不同的两点![]() (其中
(其中![]() 在
在![]() 的右侧),已知点
的右侧),已知点![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的偶函数y=f(x),满足对任意t∈R都有f(t)=f(2﹣t),且x∈(0,1]时,f(x)= ![]() ,a=f(
,a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(
),c=f( ![]() ),则( )
),则( )
A.b<c<a
B.a<b<c
C.c<a<b
D.b<a<c
查看答案和解析>>
科目:高中数学 来源: 题型:
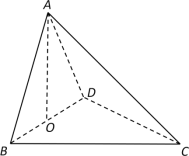
【题目】如图,将边长为2,有一个锐角为60°的菱形ABCD,沿着较短的对角线BD对折,使得![]() ,O为BD的中点.
,O为BD的中点.
(Ⅰ)求证:![]()
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求二面角A-BC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]() ,
, ![]() ,
, ![]() 的平面截该正方体所得的截面为
的平面截该正方体所得的截面为![]() ,则下列命题正确的是__________(写出所有正确命题的编号).
,则下列命题正确的是__________(写出所有正确命题的编号).

①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;
为等腰梯形;
③当![]() 时,
时, ![]() 与
与![]() 的交点
的交点![]() 满足
满足![]() ;
;
④当![]() 时,
时, ![]() 为五边形;
为五边形;
⑤当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内圆心为![]() 的圆的方程为
的圆的方程为![]() ,点
,点![]() 是圆上的动点,点
是圆上的动点,点![]() 是平面内任意一点,若线段
是平面内任意一点,若线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,则点
,则点![]() 的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com