
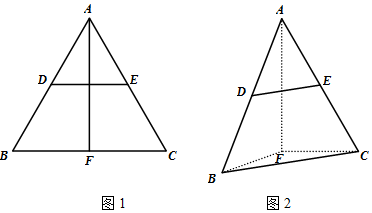
分析 (Ⅰ)推导出AF⊥BF,AF⊥FC.由此能证明AF⊥BC.
(II) 以点F为原点,在平面BCF内过点F作FC的垂线作为x轴,FC为y轴,FA为z轴,建立空间直角坐标系.利用向量法能求出二面角A-DE-F的余弦值.
(III)在平面BCF内,过F作FN⊥BF交BC于N,推导出AF⊥FN,从而FN⊥面ABF,进而面ABF⊥面DFN.由此能求出在线段BC上存在一点N,满足面ABF⊥面DFN,且 $\frac{{|{BN}|}}{{|{BC}|}}=\frac{2}{3}$.
解答 (本题满分9分)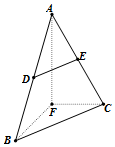
证明:(Ⅰ)∵等边△ABC,F为BC的中点,
∴AF⊥BC.
即AF⊥BF,AF⊥FC.
又∵BF∩FC=F,∴AF⊥面BCF.
又∵BC?面BCF,∴AF⊥BC. …(3分)
解:(II) 如图,以点F为原点,在平面BCF内过点F作FC的垂线作为x轴,FC为y轴,FA为z轴,建立空间直角坐标系.
设FC=2,则有F(0,0,0),$A({0,0,2\sqrt{3}})$,$B({\sqrt{3},-1,0})$,C(0,2,0),
∴$D({\frac{{\sqrt{3}}}{2},-\frac{1}{2},\sqrt{3}})$,$E({0,1,\sqrt{3}})$.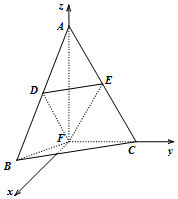
∴$\overrightarrow{FD}=({\frac{{\sqrt{3}}}{2},-\frac{1}{2},\sqrt{3}})$,$\overrightarrow{FE}=({0,1,\sqrt{3}})$,$\overrightarrow{AD}=({\frac{{\sqrt{3}}}{2},-\frac{1}{2},-\sqrt{3}})$,$\overrightarrow{AE}=({0,1,-\sqrt{3}})$.
设平面DEF的法向量为$\overrightarrow{m}$=(x1,y1,z1),
因此$\left\{\begin{array}{l}{\overrightarrow{FD}•\overrightarrow{m}=0}\\{\overrightarrow{FE}•\overrightarrow{m}=0}\end{array}\right.$,即$\left\{\begin{array}{l}\frac{{\sqrt{3}}}{2}{x_1}-\frac{1}{2}{y_1}+\sqrt{3}{z_1}=0\\{y_1}+\sqrt{3}{z_1}=0.\end{array}\right.$,
令z1=1,则$\overrightarrow{m}$=(-3,-$\sqrt{3}$,1).
设平面ADE的法向量为$\overrightarrow{n}$=(x2,y2,z2),
因此有$\left\{\begin{array}{l}{\overrightarrow{AD}•\overrightarrow{n}=0}\\{\overrightarrow{AE}•\overrightarrow{n}=0}\end{array}\right.$,即$\left\{\begin{array}{l}\frac{{\sqrt{3}}}{2}{x_2}-\frac{1}{2}{y_2}-\sqrt{3}{z_2}=0\\{y_2}-\sqrt{3}{z_2}=0.\end{array}\right.$,
令z2=1,则$\overrightarrow{n}$=(3,$\sqrt{3}$,1).
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{-11}{\sqrt{13}•\sqrt{13}}$=-$\frac{11}{13}$.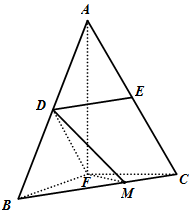
∴二面角A-DE-F的余弦值为$-\frac{11}{13}$. …(6分)
(III)在线段BC上存在一点N,满足面ABF⊥面DFN,且 $\frac{{|{BN}|}}{{|{BC}|}}=\frac{2}{3}$.
证明如下:
在平面BCF内,过F作FN⊥BF交BC于N,∵AF⊥面BCF,FN?面BCF,∴AF⊥FN.
又∵FN⊥BF,AF∩BF=F,∴FN⊥面ABF.
又∵FN?面DFN,∴面ABF⊥面DFN.
设FN=a,∵∠BFC=120°,BF=FC,∴∠FBC=∠FCB=30°.
又∵FN⊥BF,∴BN=2a.∵∠NFC=∠FCN=30°,
∴FN=NC=a.∴BC=3a.∴$\frac{BN}{BC}=\frac{2}{3}$. …(9分)
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,考查满足条件的点的位置的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
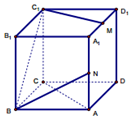 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是( )
图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得x2-2x-3>0成立 | B. | ?x0∈R,使得x2-2x-3≥0成立 | ||
| C. | ?x∈R,x2-2x-3<0恒成立 | D. | ?x∈R,x2-2x-3≥0恒成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{7}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com