
����Ŀ���ֽ�ijУ�߶��꼶ij���ѧҵˮƽ������ѧ�ɼ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���飬���ƶ��ɵľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���£����ڹ����������Ҷͼ�в��ֱ���Ƶ�ʷֲ�ֱ��ͼҲ����������ݴ˽���������⣺��ע���ð�ͬѧ��ѧ�ɼ���������
���飬���ƶ��ɵľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���£����ڹ����������Ҷͼ�в��ֱ���Ƶ�ʷֲ�ֱ��ͼҲ����������ݴ˽���������⣺��ע���ð�ͬѧ��ѧ�ɼ���������![]() �ڣ�
�ڣ�

��1����Ƶ�ʷֲ�ֱ��ͼ����������
��2���ð�ϣ���齨������ѧѧϰ����С�飬������ѧ�ɼ���õ���λͬѧ�ֱ��������鳤�����˴γɼ�����60�ֵ�ͬѧ��Ϊ��Աƽ���ֵ����飬��ÿ����һ���鳤�������ɼ���60�ֵ���Ա����˴ο��Գɼ�Ϊ52�֡�54�ֺ�98�ֵ�����ͬѧ�ֵ�ͬһ��ĸ��ʣ�
���𰸡���1��Ƶ�ʷֲ�ֱ��ͼ�����������2��![]() ��
��
��������
��1���ɾ�Ҷͼ�óɼ���![]() �е�����Ϊ4��,��Ƶ�ʷֲ�ֱ��ͼ�óɼ���
�е�����Ϊ4��,��Ƶ�ʷֲ�ֱ��ͼ�óɼ���![]() �е����������Ƶ��Ϊ0.08,�Ӷ�������Ϊ50��,�ɴ��ܰ�Ƶ�ʷֲ�ֱ��ͼ��������.
�е����������Ƶ��Ϊ0.08,�Ӷ�������Ϊ50��,�ɴ��ܰ�Ƶ�ʷֲ�ֱ��ͼ��������.
��2����ɼ�Ϊ98�ֵ�ͬѧͬ�������ͬѧ������6�ֿ���,�ɴ�������˴ο��Գɼ�Ϊ52�֡�54�ֺ�98�ֵ�����ѧ��ǡ�÷ֵ�ͬһ��ĸ���.
��1���ɾ�Ҷͼ�óɼ���![]() �е�����Ϊ4��,
�е�����Ϊ4��,
��Ƶ�ʷֲ�ֱ��ͼ�óɼ���![]() �е����������Ƶ��Ϊ
�е����������Ƶ��Ϊ![]() ,
,
��������Ϊ![]() ��,
��,
��ɼ���![]() �������Ϊ
�������Ϊ![]() ���ˣ�,
���ˣ�,
��Ƶ�ʷֲ�ֱ��ͼ�гɼ���![]() ��
��![]() ��߶ȷֱ�Ϊ��
��߶ȷֱ�Ϊ��
![]() ��
��![]() ,
,
��Ƶ�ʷֲ�ֱ��ͼ�����������£�
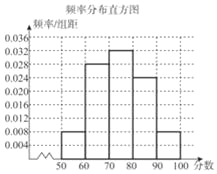
��2����ɼ�Ϊ98�ֵ�ͬѧͬ�������ͬѧ������6�ֿ��ܣ�
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
��˴ο��Գɼ�Ϊ52�֡�54�ֺ�98�ֵ�����ѧ��ǡ�÷ֵ�ͬһ��ĸ���Ϊ![]() .
.


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=aln��x+1��+x2+1��g��x��=��x2��2mx+4��
��1����a��0ʱ��������y=f��x��������б�ʵ�ȡֵ��Χ��
��2����a=��4ʱ��������x1��[0��1]��x2��[1��2]������f��x1����g��x2������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪����P-ABCD�ĵ���Ϊֱ�����Σ�AB//DC��![]() ��PA
��PA![]() ����ABCD����PA=AD=DC=
����ABCD����PA=AD=DC=![]() AB=1��M��PB���е㣮
AB=1��M��PB���е㣮
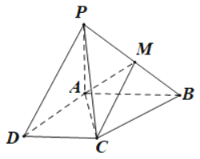
��1��֤������PAD![]() ��PCD��
��PCD��
��2����AC��PB���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ����
����![]() ʱ������
ʱ������![]() �����ԣ�
�����ԣ�
��2����![]() ���ҵ�
���ҵ�![]() ʱ������ʽ
ʱ������ʽ![]() ������
������![]() ���н⣬��ʵ��
���н⣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��һ��������1��2��3��4��5��6��7��8��9��ɵ�
��һ��������1��2��3��4��5��6��7��8��9��ɵ�![]() λ����������ͬʱ������������������
λ����������ͬʱ������������������
��1������1��2������![]() ��
��![]() �����������
�����������
��2��ÿ������ͬ������![]() ֮��ǡ��
֮��ǡ��![]() ��������
��������
��ʱ�����dz�������������![]() Ϊ�������������磬��
Ϊ�������������磬��![]() ʱ��
ʱ��![]() ������312 132����ȷ������������������
������312 132����ȷ������������������![]() ��ֵ������д��һ����Ӧ�ĺ���
��ֵ������д��һ����Ӧ�ĺ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() �����Ͻ��㵽ֱ��
�����Ͻ��㵽ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ����.��̽�����߶�
����.��̽�����߶�![]() Ϊֱ����Բ�Ƿ�����㣿����������������꣬����������˵������.
Ϊֱ����Բ�Ƿ�����㣿����������������꣬����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������ij���Ϊ������ɫ���С��ṩ�˼���ķ��㣬ij����������˾��Mobike���ƻ��ڼס����������й�Ͷ��120��Ԫ��������ҵ�涨��ÿ����������ҪͶ��40��Ԫ����ǰ���г����п�֪���׳�������P��Ͷ��![]() ����λ����Ԫ������
����λ����Ԫ������![]() ���ҳ�������Q��Ͷ��
���ҳ�������Q��Ͷ��![]() ����λ����Ԫ������
����λ����Ԫ������![]() ����׳��е�Ͷ��Ϊ
����׳��е�Ͷ��Ϊ![]() ����λ����Ԫ�����������е�������Ϊ
����λ����Ԫ�����������е�������Ϊ![]() ����λ����Ԫ����
����λ����Ԫ����
��1�����׳���Ͷ��50��Ԫʱ�����ʱ��˾�����棻
��2��������ΰ��żס����������е�Ͷ�ʣ�����ʹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ����A��B���ֲ�Ʒ�������г������Ԥ�⣬A��Ʒ��������Ͷ�ʶ�����ȣ������ϵ��Ϊ![]() �����ϵ��ͼ1��B��Ʒ��������Ͷ�ʶ������ƽ���������ȣ������ϵ��Ϊ
�����ϵ��ͼ1��B��Ʒ��������Ͷ�ʶ������ƽ���������ȣ������ϵ��Ϊ![]() �����ϵ��ͼ2����ע��������Ͷ�ʶλ����Ԫ��
�����ϵ��ͼ2����ע��������Ͷ�ʶλ����Ԫ��
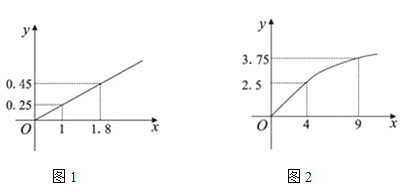
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʶ�ĺ����������![]()
![]() ��ֵ��д�����ǵĺ�����ϵʽ��
��ֵ��д�����ǵĺ�����ϵʽ��
��2������ҵ�ѳO��10��Ԫ�ʽ𣬲�ȫ��Ͷ��A��B���ֲ�Ʒ���������ʣ�����������10��ԪͶ�ʶ����ʹ��ҵ�������������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������أ������Ĺ����������ܵ������ص�Ӱ�죬��θ��ƿ��������ѳ�Ϊ������ȵ����⣬ij�������������쳧������Ͷ������ij�ͺŵĿ����������������������������۾���õ������й��������۵�ͳ�ƹ��ɣ�ÿ�������ͺſ���������![]() ����̨�������ܳɱ�Ϊ
����̨�������ܳɱ�Ϊ![]() ����Ԫ�������й̶��ɱ�Ϊ12��Ԫ������ÿ����1��̨�������ɱ�Ϊ10��Ԫ���ܳɱ�=�̶��ɱ�+�����ɱ�������������
����Ԫ�������й̶��ɱ�Ϊ12��Ԫ������ÿ����1��̨�������ɱ�Ϊ10��Ԫ���ܳɱ�=�̶��ɱ�+�����ɱ�������������![]() ����Ԫ������
����Ԫ������![]() ���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
��1����������![]() �Ľ���ʽ������=��������-�ܳɱ�����
�Ľ���ʽ������=��������-�ܳɱ�����
��2�������������ٰ�̨��Ʒʱ����ʹ������ࣿ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com