
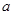 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。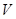 表示为
表示为 的函数;(2)
的函数;(2) 多大时,方盒的容积
多大时,方盒的容积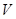 最大?
最大? 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源:不详 题型:解答题
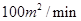 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火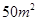 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟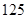 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人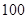 元,而每烧毁
元,而每烧毁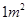 森林的损失费为
森林的损失费为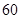 元,设消防队派了
元,设消防队派了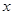 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时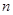
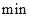 .
.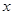 与
与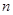 的关系式;
的关系式;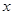 为何值时,才能使总损失最小.
为何值时,才能使总损失最小.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的定义域为R,其导函数
的定义域为R,其导函数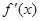 的图像如图所示,则对于任意
的图像如图所示,则对于任意 ,
,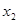
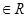 (
( ),下列结论正确的是( )
),下列结论正确的是( )
 <0恒成立 ②
<0恒成立 ② ;③
;③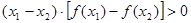 ;
; ;⑤
;⑤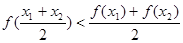 。
。| A.①③ | B.①③④ | C.②④ | D.②⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com