【题目】为改善环境，节约资源，我国自2019年起在全国地级及以上城市全面启动生活垃圾分类，垃圾分类已成为一种潮流.某市一小区的主管部门为了解居民对垃圾分类的认知是否与其受教育程度有关，对该小区居民进行了随机抽样调查，得到如下统计数据的列联表：
知道如何对垃圾进行分类 | 不知道如何对垃圾进行分类 | 合计 | |
未受过高等教育 |
| 10 |
|
受过高等教育 |
|
|
|
合计 |
|
| 50 |
（1）求列联表中的
，
，
，
，
的值，并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率；
（2）根据列联表判断能否有
的把握认为该小区居民对垃圾分类的认知与其受教育程度有关？
参考数据及公式：
|
|
|
|
|
|
|
|
|
|
|
|
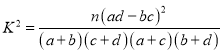，其中
.
科目：高中数学 来源： 题型：
【题目】“新冠肺炎”疫情的控制需要根据大数据进行分析，并有针对性的采取措施.下图是甲、乙两个省份从2月7日到2月13日一周内的新增“新冠肺炎”确诊人数的折线图.根据图中甲、乙两省的数字特征进行比对，下列说法错误的是（ ）
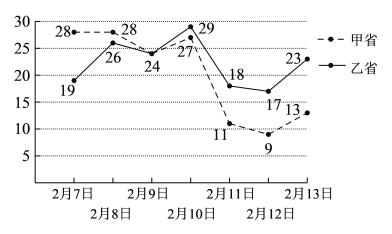
A.2月7日到2月13日甲省的平均新增“新冠肺炎”确诊人数低于乙省
B.2月7日到2月13日甲省的单日新增“新冠肺炎”确诊人数最大值小于乙省
C.2月7日到2月13日乙省相对甲省的新增“新冠甲省肺炎”确诊人数的波动大
D.后四日（2月10日至13日）乙省每日新增“新冠肺炎”确诊人数均比甲省多
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】椭圆
：
的左、右焦点分别是
，
，离心率为
，左、右顶点分别为
，
.过且垂直于
轴的直线被椭圆截得的线段长为1.
（1）求椭圆的标准方程；
（2）经过点
的直线与椭圆相交于不同的两点
、
（不与点、重合），直线
与直线
相交于点
，求证：、、三点共线.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“地摊经济”是李克强总理在本届政府工作报告中向全国人民发出的口号，某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据
（
，2，3，4，5，6），如表所示：
试销单价x（元） | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y（件） | q | 84 | 83 | 80 | 75 | 68 |
已知
，
，
（1）试求q，若变量x，y具有线性相关关系，求产品销量y（件）关于试销单价x（元）的线性回归方程
；
（2）用
表示用（1）中所求的线性回归方程得到的与
对应的产品销量的估计值.当销售数据对应的残差的绝对值
时，则将销售数据称为一个“好数据”.现从6个销售数据中任取3个，求“好数据”个数
的分布列和数学期望
.
（参考公式：线性回归方程中
，
的最小二乘估计分别为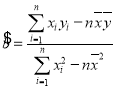
，
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
