
(本题满分12分)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.

解:(1)百米成绩在[16,17)内的频率为0.32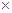 1=0.32. 0.32
1=0.32. 0.32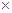 1000=320
1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人。 ……2分
(2)设图中从左到右前3个组的频率分别为3x,8x ,19x 依题意,得 3x+8x+19x+0.32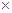 1+0.08
1+0.08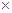 1=1
,∴x=0.02 ……4分
1=1
,∴x=0.02 ……4分
设调查中随机抽取了n 个学生的百米成绩,则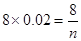 ∴n=50
∴n=50
∴调查中随机抽取了50个学生的百米成绩. ……6分
(3)百米成绩在第一组的学生数有3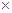 0.02
0.02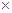 1
1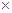 50=3,记他们的成绩为a,b,c
50=3,记他们的成绩为a,b,c
百米成绩在第五组的学生数有0.08 1
1 50=
4,记他们的成绩为m,n,p,q
50=
4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21个 ……9分
其中满足成绩的差的绝对值大于1秒所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个,……10分
所以P=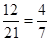 ……12分
……12分
【解析】略


科目:高中数学 来源: 题型:
(本题满分12分)
为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?w.w.w.k.s.5.u.c.o.m ![]()
|
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,![]() 还喜欢打羽毛球,
还喜欢打羽毛球,![]() 还喜欢打乒乓球,
还喜欢打乒乓球,![]() 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学文) 题型:解答题
(本题满分12分)
为预防 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
|
|
A组 |
B组 |
C组 |
|
疫苗有效 |
673 |
|
|
|
疫苗无效 |
77 |
90 |
|
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知 ,求不能通过测试的概率.
,求不能通过测试的概率.
查看答案和解析>>
科目:高中数学 来源:2010年陕西省高三第七次适应性考试数学(文) 题型:解答题
(本题满分12分)为研究气候的变化趋势,某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度,如下表:
(1)若第六、七、八组的频数 、
、 、
、 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出 、
、 、
、 、
、 的值;
的值;
(2)若从第一组和第八组的所有星期中随机抽取两个星期,分别记它们的平均温度为 ,
, ,求事件“
,求事件“ ”的概率.
”的概率.

查看答案和解析>>
科目:高中数学 来源:2010年甘肃省天水市高一期中考试数学卷 题型:解答题
(本题满分12分) 设 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)求 的最小值;
的最小值;
(3)设函数 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com