已知F1(-2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为E.
(1)求轨迹E的方程;
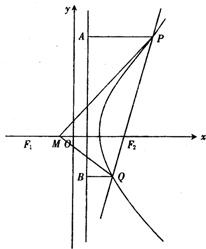
(2)若直线l过点F2且与轨迹E交于P、Q两点.无论直线l绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
分析:(1)由条件知,点P的轨迹E是以F1、F2为焦点的双曲线右支,从而写出轨迹E的方程即可.
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2),将直线的方程代入双曲线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量垂直关系即可求得m值,从而解决问题.
解答:解:(1)由|PF
1|-|PF
2|=2<|F
1F
2|知,点P的轨迹E是以F
1、F
2为焦点的双曲线右支,
由c=2,2a=2,∴b
2=3,故轨迹E的方程为
x2-=1(x≥1).
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x
1,y
1),Q(x
2,y
2),
与双曲线方程联立消y得(k
2-3)x
2-4k
2x+4k
2+3=0,
∴
| | k2-3≠0 | | △>0 | | x1+x2=>0 | | x1•x2=>0 |
| |
解得k
2>3.
∵
•=(x1-m)(x2-m)+y1y2=(x
1-m)(x
2-m)+k
2(x
1-2)(x
2-2)
=(k
2+1)x
1x
2-(2k
2+m)(x
1+x
2)+m
2+4k
2=
-+m2+4k2=
+m2.(7分)
∵MP⊥MQ,∴
•=0,
故得3(1-m
2)+k
2(m
2-4m-5)=0对任意的k
2>3恒成立,
∴
,解得m=-1.
∴当m=-1时,MP⊥MQ.
当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(-1,0)知结论也成立,
综上,当m=-1时,MP⊥MQ.
点评:本题考查用待定系数法求双曲线的标准方程,利用两个向量的数量积公式及双曲线的性质解决具体问题,体现了分类讨论的数学思想.

 解得k2>3.
解得k2>3.
