
【题目】已知函数f(x)=2cos22x﹣2,给出下列命题: ①β∈R,f(x+β)为奇函数;
②α∈(0, ![]() ),f(x)=f(x+2α)对x∈R恒成立;
),f(x)=f(x+2α)对x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,则|x1﹣x2|的最小值为 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z).其中的真命题有( )
A.①②
B.③④
C.②③
D.①④
【答案】C
【解析】解:由题意,f(x)=2cos22x﹣2=cos4x﹣1;
对于①,∵f(x)=cos4x﹣1的图象如图所示:
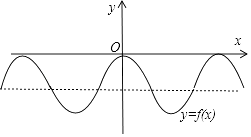
函数f(x+β)的图象是f(x)的图象向左或向右平移|β|个单位,
它不会是奇函数的,故①错误;
对于②,f(x)=f(x+2α),∴cos4x﹣1=cos(4x+8α)﹣1,
∴8α=2kπ,∴α= ![]() ,k∈Z;
,k∈Z;
又α∈(0, ![]() ),∴取α=
),∴取α= ![]() 或
或 ![]() 时,
时,
∴f(x)=f(x+2α)对x∈R恒成立,②正确;
对于③,|f(x1)﹣f(x2)|=|cos4x1﹣cos4x2|=2时,
|x1﹣x2|的最小值为 ![]() =
= ![]() =
= ![]() ,∴③正确;
,∴③正确;
对于④,当f(x1)=f(x2)=0时,
x1﹣x2=kT=k ![]() =
= ![]() (k∈Z),∴④错误;
(k∈Z),∴④错误;
综上,真命题是②③.
故选:C.
化简函数f(x),画出f(x)的图象,根据图象平移判断函数f(x+β)不是奇函数,判断①错误;
根据f(x)=f(x+2α)求出方程在α∈(0, ![]() )的解,判断②正确;
)的解,判断②正确;
由|f(x1)﹣f(x2)|=2时,|x1﹣x2|的最小值为 ![]() =
= ![]() ,判断③正确;
,判断③正确;
当f(x1)=f(x2)=0时,x1﹣x2=kT= ![]() ,判断④错误.
,判断④错误.


科目:高中数学 来源: 题型:
【题目】某公司有A、B两个景点,位于一条小路(直道)的同侧,分别距小路![]() km和2
km和2![]() km,且A、B景点间相距2 km,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳观赏和拍摄效果,则观景点应设于____.
km,且A、B景点间相距2 km,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳观赏和拍摄效果,则观景点应设于____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜欢打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为 ![]()
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附:K2= ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点).
(2)∠MPN是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 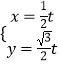 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2 ![]() ,
, ![]() ). (Ⅰ)求直线l以及曲线C的极坐标方程;
). (Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y+1=0,l2:-2x+y+2=0,它们相交于点A.
(1)判断直线l1和l2是否垂直?请给出理由.
(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com