
【题目】已知直线l经过点P(﹣2,5),且斜率为﹣ ![]()
(1)求直线l的方程;
(2)若直线m与l平行,且点P到直线m的距离为3,求直线m的方程.
【答案】
(1)解:由点斜式写出直线l的方程为 y﹣5=﹣ ![]() (x+2),化简为 3x+4y﹣14=0.
(x+2),化简为 3x+4y﹣14=0.
(2)解:由直线m与直线l平行,可设直线m的方程为3x+4y+c=0,
由点到直线的距离公式,得 ![]() ,即
,即 ![]() ,
,
解得c=1或c=﹣29,故所求直线方程 3x+4y+1=0,或 3x+4y﹣29=0.
【解析】(1)由点斜式写出直线l的方程为 y﹣5=﹣ ![]() (x+2),化为一般式.(2)由直线m与直线l平行,可设直线m的方程为3x+4y+c=0,由点到直线的距离公式求得待定系数c 值,即得所求直线方程.
(x+2),化为一般式.(2)由直线m与直线l平行,可设直线m的方程为3x+4y+c=0,由点到直线的距离公式求得待定系数c 值,即得所求直线方程.
【考点精析】利用直线的斜率和一般式方程对题目进行判断即可得到答案,需要熟知一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα;直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知![]() +
+![]() =1(a>>0)点A(1,
=1(a>>0)点A(1,![]() )是离心率为
)是离心率为![]() 的椭圆C:上的一点,斜率为
的椭圆C:上的一点,斜率为![]() 的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.
的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△ABD面积的最大值;
(Ⅲ)设直线AB、AD的斜率分别为k1 , k2 , 试问:是否存在实数λ,使得k1+λk2=0成立?若存在,求出λ的值;否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数).
为参数).
(1)直线![]() 过
过![]() 且与曲线
且与曲线![]() 相切,求直线
相切,求直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 与点
与点![]() 关于
关于![]() 轴对称,求曲线
轴对称,求曲线![]() 上的点到点
上的点到点![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(![]() ,-2).
,-2).
(1)求φ的值;
(2)若f(![]() )=
)=![]() ,-
,-![]() <α<0,求sin(2α-
<α<0,求sin(2α-![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , a1=10,an+1=9Sn+10.
(1)求证:{lgan}是等差数列;
(2)设Tn是数列{ ![]() }的前n项和,求Tn;
}的前n项和,求Tn;
(3)求使Tn> ![]() (m2﹣5m)对所有的n∈N*恒成立的整数m的取值集合.
(m2﹣5m)对所有的n∈N*恒成立的整数m的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点,求证: 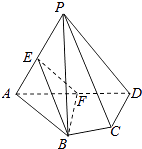
(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如表:
(单位:万件)之间的关系如表:


(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合![]() 与
与![]() 的回归模型,并用相关系数甲乙说明;
的回归模型,并用相关系数甲乙说明;
(Ⅲ)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量约为多少?.
的回归方程,预测第5年的销售量约为多少?.
附注:参考数据: 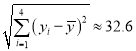 ,
, ![]() ,
, ![]() .
.
参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( ) 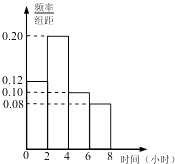
A.1.78小时
B.2.24小时
C.3.56小时
D.4.32小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com