
直线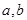 为异面直线,直线
为异面直线,直线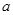 上有4个点,直线
上有4个点,直线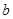 上有5个点,以这些点为顶点的三角形共有 个;
上有5个点,以这些点为顶点的三角形共有 个;
70
解析试题分析:因为直线a上有4个点,所以,可以组成线段的条数是:3+2+1=6(条),直线a上的一个点和直线b的一条线段构成三角形的个数是:6×5=30(个),又因为,直线b上有5个点,所以,可以组成线段的条数是:4+3+2+1=10(个),直线b上的一条线段和直线a上的一个点构成三角形的个数是:10×4=40(个),共有三角形的个数:30+40=70(个),故以这些点为顶点可以画出70个三角形.
考点:本题考查了简单的排列组合问题
点评:运用加法原理(做一件事情,完成它有N类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,…,在第N类办法中有mn种不同的方法,那么完成这件事情共有m1+m2+…+mn种不同的方法)和乘法原理(做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2不同的方法,…,做第n步有mn不同的方法.那么完成这件事共有 N=m1m2m3…mn 种不同的方法)即可.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
某中学在高一年级开设了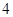 门选修课,每名学生必须参加这
门选修课,每名学生必须参加这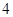 门选修课中的一门,对于该年级的甲、乙、丙
门选修课中的一门,对于该年级的甲、乙、丙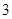 名学生,这
名学生,这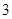 名学生选择的选修课互不相同的概率是 (结果用最简分数表示).
名学生选择的选修课互不相同的概率是 (结果用最简分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知从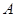 地到
地到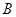 地有2条公路可走,从
地有2条公路可走,从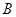 地到
地到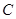 地有3条小路可走,又从
地有3条小路可走,又从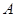 地不过
地不过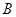 地到
地到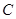 地有1条水路可走,那么从
地有1条水路可走,那么从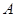 地到
地到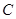 地的不同走法一共有______________种.
地的不同走法一共有______________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com